
����Ŀ��������С����Ƶ�����������һ��������һ���㣬ʹ���������ε��������㹹�ɵ���������ԭ�������������ij߹���ͼ���̣�
��֪����ABC��
��������BC��������һ��P��ʹ����PAC�ס�ABC��
��������ͼ��
�����߶�AC�Ĵ�ֱƽ����GH��
�����߶�AB�Ĵ�ֱƽ����EF����GH�ڵ�O��
���Ե�OΪԲ�ģ���OAΪ�뾶��Բ��
���Ե�CΪԲ�ģ�CAΪ�뾶����������O�ڵ�D�����A���غϣ���
�������߶�AD��BC�ڵ�P��
���Ե�P�����������ĵ㣮
����С����Ƶij߹���ͼ���̣�
��1��ʹ��ֱ�ߺ�Բ�棬��ȫͼ�Σ���������ͼ�ۼ���
��2����������֤����
֤������CD��AC��
��![]() ���� ����
���� ����
����� �������� ����
�֡ߡ��� �������� ����
���PAC�ס�ABC���� �����������������ݣ���

���𰸡���1������������2��![]() ��CAP��ABC��ACP��BCA��������Ƕ�Ӧ��ȵ���������������
��CAP��ABC��ACP��BCA��������Ƕ�Ӧ��ȵ���������������
��������
(1)������Ŀ����������⼴�ɣ�
(2)����CD������ͼ֪��AC��CD��,�ɵá�CAP����ABC������ACP����BCA��
�ɵ���ACP�ס�BCA��������Ƕ�Ӧ��ȵ��������������ƣ�.
�⣺��1����ȫͼ����ͼ��ʾ��

��2������CD������ͼ֪��AC��CD��
��![]() =
=![]() ��
��
���CAP����ABC��
�ߡ�ACP����BCA��
���ACP�ס�BCA��������Ƕ�Ӧ��ȵ��������������ƣ���
�ʴ�Ϊ��![]() ��CAP��ABC��ACP��BCA��������Ƕ�Ӧ��ȵ��������������ƣ�
��CAP��ABC��ACP��BCA��������Ƕ�Ӧ��ȵ��������������ƣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
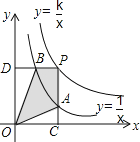
����Ŀ������������y=![]() ��y=
��y=![]() �ڵ�һ�����ڵ�ͼ����ͼ��ʾ����P��y=
�ڵ�һ�����ڵ�ͼ����ͼ��ʾ����P��y=![]() ��ͼ���ϣ�PC��x�ᣬ��y=
��ͼ���ϣ�PC��x�ᣬ��y=![]() ��ͼ���ڵ�A��PD��y�ᣬ��y=
��ͼ���ڵ�A��PD��y�ᣬ��y=![]() ��ͼ���ڵ�B������P��y=
��ͼ���ڵ�B������P��y=![]() ��ͼ�����˶�ʱ�����½��ۣ�����ODB����OCA�������ȣ���PA��PBʼ����ȣ����ı���PAOB��������ᷢ���仯���ܵ���A��PC���е�ʱ����Bһ����PD���е㣮����һ����ȷ���ǣ�������
��ͼ�����˶�ʱ�����½��ۣ�����ODB����OCA�������ȣ���PA��PBʼ����ȣ����ı���PAOB��������ᷢ���仯���ܵ���A��PC���е�ʱ����Bһ����PD���е㣮����һ����ȷ���ǣ�������
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
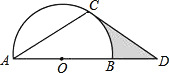
����Ŀ����ͼ����D����O��ֱ��AB���ӳ����ϣ���C����O�ϣ�AC=CD����ACD=120��.
��1����֤��CD����O�����ߣ�
��2������O�İ뾶Ϊ2����ͼ����Ӱ���ֵ����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
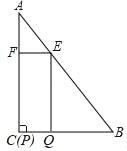
����Ŀ����ͼ���ڡ�ABC�У���A��30�㣬��C��90�㣬AB��12���ı���EFPQ�Ǿ��Σ���P���C�غϣ���Q��E��F�ֱ���BC��AB��AC�ϣ���E���A����B�����غϣ���
��1����AE��8ʱ����EF�ij���
��2����AE��x������EFPQ�����Ϊy��
����y��x�ĺ�����ϵʽ��
����xΪ��ֵʱ��y�����ֵ�����ֵ�Ƕ��٣�
��3��������EFPQ��������ʱ��������EFPQ��ÿ��1����λ���ٶ�������CB���������˶�������P�����Bʱֹͣ�˶��������˶�ʱ��Ϊt�룬����EFPQ���ABC�ص����ֵ����ΪS����S��t�ĺ�����ϵʽ����д��t��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
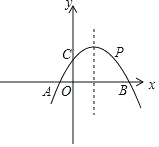
����Ŀ����ͼ����֪������y��ax2+bx+1��x��ֱ���A(��1��0)��B(3��0)����y�ύ�ڵ�C��
(1)�������߽���ʽ��
(2)��ֱ��BC�Ϸ������������е�P��ʹ��PBC���Ϊ1�������P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
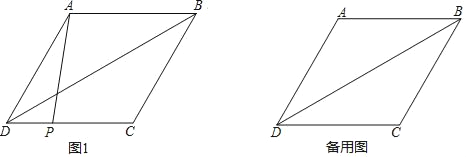
����Ŀ��������ABCD�У���ADC��60�㣬BD��һ���Խ��ߣ���P�ڱ�CD�ϣ����C��D���غϣ�������AP��ƽ����ADP��ʹ��D�ƶ�����C���õ���BCQ����BD��ȡһ��H��ʹHQ��HD������HQ��AH��PH��
��1�������ⲹȫͼ1��
��2���ж�AH��PH��������ϵ����AHP�Ķ�����������֤����
��3������AHQ��141��������ABCD�ı߳�Ϊ1����д����DP����˼·�������Բ�д����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
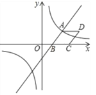
����Ŀ����ͼ����֪һ�κ��� y��![]() x��3 �뷴�������� y��
x��3 �뷴�������� y��![]() ��ͼ���ཻ�ڵ� A��4��n������ x ���ཻ�ڵ� B��
��ͼ���ཻ�ڵ� A��4��n������ x ���ཻ�ڵ� B��
(1)�� n �� k ��ֵ��
(2)�� AB Ϊ�������� ABCD��ʹ�� C �� x ���������ϣ��� D �ڵ�һ���ޣ���� D �����ꣻ
(3)�۲췴��������y=![]() ��ͼ�� y����2 ʱ����ֱ��д���Ա��� x ��ȡֵ��Χ��
��ͼ�� y����2 ʱ����ֱ��д���Ա��� x ��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һ�������Ĵ�����װ��7��ֻ����ɫ��ͬ��������2������5������
��1����Ӵ����������һ�����Ǻ���ĸ��ʣ�
��2���Ӵ����������һ����¼��ɫ��Żأ�ҡ�ȣ����������һ������������������ǡ����ɫ��ͬ�ĸ��ʣ�
��3�����Ӵ���ȡ�����ɸ���������ͬ�����Ļ�������Ⱥ�ʹ������Ӵ���������������ɫ��һ��һ�Ƶĸ���Ϊ![]() ��������м����������˻���
��������м����������˻���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�͡�ADE���ǵ���ֱ�������Σ���BAC����DAE��90�㣬AB��AC��2��OΪAC�е㣬����D��ֱ��BC���˶�������OE�����ڵ�D�˶������У��߶�OE����Сֵ��Ϊ_____��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com