
【题目】定义:有一组对角相等而另一组对角不相等的凸四边形叫做“等对角四边形”.
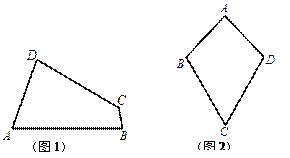
(1)已知:如图1,四边形![]() 是“等对角四边形”,
是“等对角四边形”, ![]() ,
, ![]() ,
, ![]() .求
.求![]() ,
, ![]() 的度数.
的度数.
(2)在探究“等对角四边形”性质时:
① 小红画了一个“等对角四边形”![]() (如图2),其中
(如图2),其中![]() ,
, ![]() ,此时她发现
,此时她发现![]() 成立.请你证明此结论.
成立.请你证明此结论.
② 由此小红猜想:“对于任意‘等对角四边形’,当一组邻边相等时,另一组邻边也相等”.你认为她的猜想正确吗?若正确,请证明;若不正确,请举出反例.
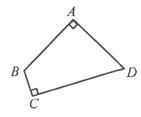
(3)已知:在“等对角四边形”![]() 中,
中, ![]() ,
, ![]() ,AB=AD=4,.求∠D和对角线
,AB=AD=4,.求∠D和对角线![]() 的长.
的长.
【答案】(1)130°;(2)①证明见解析;②不正确;(3)∠D=90°,AC=8
【解析】试题分析:(1)根据四边形ABCD是“等对角四边形”得出∠D=∠B=80°,根据多边形内角和定理求出∠C即可;
(2)①连接BD,根据等边对等角得出∠ABD=∠ADB,求出∠CBD=∠CDB,根据等腰三角形的判定得出即可;
②不正确.举一个反例即可.
(3)分两种情况:①当∠ADC=∠ABC=90°时,连接AC,易证⊿ABC≌⊿ADC,得出∠BCA=30°,利用30°所对的直角边等于斜边的一半,从而求出AC;
②当∠BCD=∠DAB=120°时,不成立.
试题解析:(1)∵等对角四边形ABCD中,∠A≠∠C,∠B=80°,
∴∠D=∠B=80°.
∵∠A=70°,
∴![]() .
.
(2)①如图,连接BD,
∵AB=AD,∴![]() .
.
∵![]() ,∴
,∴![]() .
.
∴CB=CD.

②不正确,反例如图,∠A=∠C=90°,AB=AD,但CB≠CD.
(3)分两种情况:
①当∠ADC=∠ABC=90°时,连接AC,

∵AD=AB,
∴Rt⊿ADC≌Rt⊿ABC,
∴∠ACD=∠ACB=30°
在Rt⊿ABC中,∠ACB=30°,AB=4,
∴AC=2AB=2×4=8;
②当∠BCD=∠DAB=120°时,不成立.


科目:初中数学 来源: 题型:
【题目】(11·大连)某农科院对甲、乙两种甜玉米各用10块相同条件的试验田进行试验,
得到两个品种每公顷产量的两组数据,其方差分别为s甲2=0.002、s乙2=0.03,则 ( )
A.甲比乙的产量稳定 B.乙比甲的产量稳定
C.甲、乙的产量一样稳定D.无法确定哪一品种的产量更稳定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某景点试开放期间,团队收费方案如下:不超过30人时,人均收费120元;超过30人且不超过m(30<m≤100)人时,每增加1人,人均收费降低1元;超过m人时,人均收费都按照m人时的标准.设景点接待有x名游客的某团队,收取总费用为y元.
(1)求y关于x的函数表达式;
(2)景点工作人员发现:当接待某团队人数超过一定数量时,会出现随着人数的增加收取的总费用反而减少这一现象.为了让收取的总费用随着团队中人数的增加而增加,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点P、Q分别是等边△ABC边AB、BC上的动点(端点除外),点P从顶点A、点Q从顶点B同时出发,且它们的运动速度相同,连接AQ、CP交于点M.
(1)求证:△ABQ≌△CAP;
(2)当点P、Q分别在AB、BC边上运动时,∠QMC变化吗?若变化,请说明理由;若不变,求出它的度数.
(3)如图2,若点P、Q在运动到终点后继续在射线AB、BC上运动,直线AQ、CP交点为M,则∠QMC变化吗?若变化,请说明理由;若不变,直接写出它的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一个直角三角形纸片ACB,其中∠ACB=90°,AC=4,BC=3,E、F分别是AC、AB边上点,连接EF.
(1)图①,若将纸片ACB的一角沿EF折叠,折叠后点A落在AB边上的点D处,且使S四边形ECBF=3S△EDF,求AE的长;
(2)如图②,若将纸片ACB的一角沿EF折叠,折叠后点A落在BC边上的点M处,且使MF∥CA.
①试判断四边形AEMF的形状,并证明你的结论;
②求EF的长;
(3)如图③,若FE的延长线与BC的延长线交于点N,CN=1,CE=![]() ,求
,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
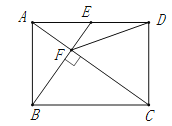
【题目】如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,分析下列四个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=.其中正确的结论有( )
A.4个 B.3个 C.2个 D.1个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com