
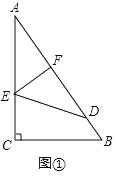
����Ŀ����ͼ����֪һ��ֱ��������ֽƬACB�����С�ACB=90�㣬AC=4��BC=3��E��F�ֱ���AC��AB���ϵ㣬����EF��
��1��ͼ�٣�����ֽƬACB��һ����EF�۵����۵����A����AB���ϵĵ�D������ʹS�ı���ECBF=3S��EDF����AE�ij���
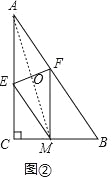
��2����ͼ�ڣ�����ֽƬACB��һ����EF�۵����۵����A����BC���ϵĵ�M������ʹMF��CA��
�����ж��ı���AEMF����״����֤����Ľ��ۣ�
����EF�ij���
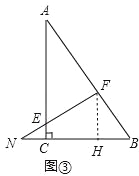
��3����ͼ�ۣ���FE���ӳ�����BC���ӳ��߽��ڵ�N��CN=1��CE=![]() ����
����![]() ��ֵ��
��ֵ��

���𰸡���1��![]() ����2�����ı���AEMFΪ���������������������
����2�����ı���AEMFΪ���������������������![]() ����3��
����3��![]() ��
��
��������
�����������1���������۵������ʵõ�EF��AB����AEF�ա�DEF����S��AEF��S��DEF������S��ABC=4S��AEF����֤��Rt��AEF��Rt��ABC��Ȼ��������������ε����ʵõ�![]() =��
=��![]() ��2�������ù��ɶ������AB���ɵõ�AE�ij�����2����ͨ��֤������������ж��ı���AEMFΪ���Σ�
��2�������ù��ɶ������AB���ɵõ�AE�ij�����2����ͨ��֤������������ж��ı���AEMFΪ���Σ�
������AM��EF�ڵ�O����ͼ�ڣ���AE=x����EM=x��CE=4��x����֤����CME�ס�CBA�õ�![]() =
=![]() =
=![]() �����x������CM=
�����x������CM=![]() �������ù��ɶ��������AM��Ȼ��������ε������ʽ����EF��
�������ù��ɶ��������AM��Ȼ��������ε������ʽ����EF��
��3����ͼ�ۣ���FH��BC��H����֤����NCE�ס�NFH���������Ʊȵõ�FH��NH=4��7����FH=4x��NH=7x����CH=7x��1��BH=3����7x��1��=4��7x����֤����BFH�ס�BAC���������Ʊȿɼ����x=![]() ����ɼ����FH��BH���������ù��ɶ��������BF���Ӷ��õ�AF�ij������ǿɼ����
����ɼ����FH��BH���������ù��ɶ��������BF���Ӷ��õ�AF�ij������ǿɼ����![]() ��ֵ��
��ֵ��
�����������1����ͼ�٣�
�ߡ�ACB��һ����EF�۵����۵����A����AB���ϵĵ�D����
��EF��AB����AEF�ա�DEF��
��S��AEF��S��DEF��
��S�ı���ECBF=3S��EDF��
��S��ABC=4S��AEF��
��Rt��ABC�У��ߡ�ACB=90�㣬AC=4��BC=3��
��AB=![]() =5��
=5��
�ߡ�EAF=��BAC��
��Rt��AEF��Rt��ABC��
��![]() =��
=��![]() ��2������
��2������![]() ��2=
��2=![]() ��
��
��AE=![]() ��
��
��2�����ı���AEMFΪ���Σ��������£�
��ͼ�ڣ��ߡ�ACB��һ����EF�۵����۵����A����AB���ϵĵ�D����
��AE=EM��AF=MF����AFE=��MFE��
��MF��AC��
���AEF=��MFE��
���AEF=��AFE��
��AE=AF��
��AE=EM=MF=AF��
���ı���AEMFΪ���Σ�
������AM��EF�ڵ�O����ͼ�ڣ�
��AE=x����EM=x��CE=4��x��
���ı���AEMFΪ���Σ�
��EM��AB��
���CME�ס�CBA��
��![]() =
=![]() =
=![]() ����
����![]() =
=![]() =
=![]() �����x=
�����x=![]() ��CM=
��CM=![]() ��
��
��Rt��ACM��AM=![]() =
=![]() =
=![]() ��
��
��S����AEMF=![]() EFAM=AECM��
EFAM=AECM��
��EF=2��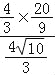 =
=![]() ��
��
��3����ͼ�ۣ���FH��BC��H��
��EC��FH��
���NCE�ס�NFH��
��CN��NH=CE��FH����1��NH=![]() ��FH��
��FH��
��FH��NH=4��7��
��FH=4x��NH=7x����CH=7x��1��BH=3����7x��1��=4��7x��
��FH��AC��
���BFH�ס�BAC��
��BH��BC=FH��AC������4��7x����3=4x��4�����x=![]() ��
��
��FH=4x=![]() ��BH=4��7x=
��BH=4��7x=![]() ��
��
��Rt��BFH��BF=![]() =2��
=2��
��AF=AB��BF=5��2=3��
��![]() =
=![]() ��
��


 ����ѧҵ���Ե�����ϵ�д�
����ѧҵ���Ե�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ĺͱ����֤��������������ȵ��������ǵ�������������һ����ʱ������ͼ�Σ�д������֪��������֤������ͼ�������ǶԸ��������ĸ������������£�
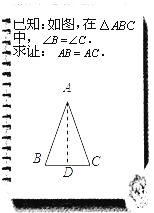
������������A��BC���д���AD������ΪD����
���������ABC�Ľ�ƽ����AD����
��ѧ��ʦ������λͬѧ�ĸ�����������˵����������������ȷ�ģ������ĵ�������Ҫ��������
��1�������Ҫ˵�����ĵĸ����������������
��2�����ݱ��ĸ��������������֤�����̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺��һ��Խ���ȶ���һ��ԽDz�������ı��ν������ȶԽ��ı��Ρ���
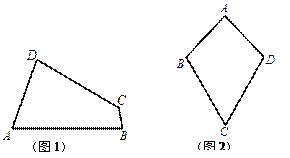
��1����֪����ͼ1���ı���![]() �ǡ��ȶԽ��ı��Ρ���
�ǡ��ȶԽ��ı��Ρ��� ![]() ��
�� ![]() ��
�� ![]() ����
����![]() ��
�� ![]() �Ķ�����
�Ķ�����
��2����̽�����ȶԽ��ı��Ρ�����ʱ��
�� С�컭��һ�����ȶԽ��ı��Ρ�![]() ����ͼ2��������
����ͼ2��������![]() ��
�� ![]() ����ʱ������
����ʱ������![]() ����������֤���˽��ۣ�
����������֤���˽��ۣ�
�� �ɴ�С����룺���������⡮�ȶԽ��ı��Ρ�����һ���ڱ����ʱ����һ���ڱ�Ҳ��ȡ�������Ϊ���IJ�����ȷ������ȷ����֤����������ȷ����ٳ�������
��3����֪���ڡ��ȶԽ��ı��Ρ�![]() �У�
�� ![]() ��
�� ![]() ��AB=AD=4�������D�ͶԽ���
��AB=AD=4�������D�ͶԽ���![]() �ij���
�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABCD�У��Խ���AC��BD�ཻ�ڵ�O����OA=OB��
��1����֤���ı���ABCD�Ǿ��Σ�
��2����AD=4����AOD=60������AB�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����й��ڷ�ʽ����������˵����ȷ���ǣ� ��
A.ʹ���еķ�ĸ��ֵ��Ϊ��Ľ�������
B.��ʽ���̵Ľ�Ϊ���������
C.ʹ���ӵ�ֵΪ��Ľ��������
D.ʹ���ĸ��ֵΪ��Ľ�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����м�����ȷ���ǣ� ��
A.a+a=2a
B.b3b3=2b3
C.a3��a=a3
D.��a5��2=a7
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
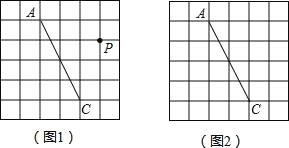
����Ŀ��ͼ1��ͼ2��������״�ʹ�С��ȫ��ͬ�ķ���ֽ������ֽ��ÿ��С�����εı߳���Ϊ1���߶�AC�������˵����С�����εĶ����ϣ�
��1����ͼ1����P��С�����εĶ����ϣ���ͼ1��������P����ֱ��AC�ĶԳƵ�Q������AQ��QC��CP��PA����ֱ��д���ı���AQCP���ܳ���
��2����ͼ2�л���һ�����߶�ACΪ�Խ��ߡ����Ϊ6�ľ���ABCD���ҵ�B�͵�D����С�����εĶ����ϣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������ѧ����˰�43��ͬѧ��ͥ�˿ڵ�ͳ�Ʊ�����43����ͥ�˿ڵ���������λ���ֱ��ǣ�������
��ͥ�˿������ˣ� | 2 | 3 | 4 | 5 | 6 |
ѧ���������ˣ� | 3 | 15 | 10 | 8 | 7 |
A.5��6B.3��4C.3��5D.4��6
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com