
【题目】(1)如图甲,AB∥CD,试问∠2与∠1+∠3的关系是什么,为什么?
(2)如图乙,AB∥CD,试问∠2+∠4与∠1+∠3+∠5一样大吗?为什么?
(3)如图丙,AB∥CD,试问∠2+∠4+∠6与∠1+∠3+∠5+∠7哪个大?为什么?
你能将它们推广到一般情况吗?请写出你的结论.
【答案】解:(1)∠2=∠1+∠3.
过点E作EF∥AB,
∵AB∥CD,
∴AB∥CD∥EF,
∴∠BEF=∠1,∠CEF=∠3,
∴∠2=∠BEF+∠CEF=∠1+∠3;
(2)∠2+∠4=∠1+∠3+∠5.
分别过点E,G,M,作EF∥AB,GH∥AB,MN∥AB,
∵AB∥CD,
∴AB∥CD∥EF∥GH∥MN,
∴∠1=∠BEF,∠FEG=∠EGH,∠HGM=∠GMN,∠CMN=∠5,
∴∠2+∠4=∠BEF+∠FEG+∠GMN+∠CMN=∠1+∠EGH+∠MGH+∠5=∠1+∠3+∠5;
(3)∠2+∠4+∠6=∠1+∠3+∠5+∠7.
分别过点E,G,M,K,P,作EF∥AB,GH∥AB,MN∥AB,KL∥AB,PQ∥AB,
∵AB∥CD,
∴AB∥CD∥EF∥GH∥MN∥KL∥PQ,
∴∠1=∠BEF,∠FEG=∠EGH,∠HGM=∠GMN,∠KMN=∠LKM,∠LKP=∠KPQ,∠QPC=∠7,
∴∠2+∠4+∠6=∠1+∠3+∠5+∠7.
归纳:开口朝左的所有角度之和与开口朝右的所有角度之和相等.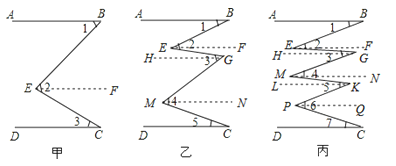
【解析】(1)首先过点E作EF∥AB,由AB∥CD,可得AB∥CD∥EF,根据平行线的性质,易得∠2=∠BEF+∠CEF=∠1+∠3;
(2)首先分别过点E,G,M,作EF∥AB,GH∥AB,MN∥AB,由AB∥CD,可得AB∥CD∥EF∥GH∥MN,由平行线的性质,可得∠2+∠4=∠1+∠3+∠5.
(3)首先分别过点E,G,M,K,P,作EF∥AB,GH∥AB,MN∥AB,KL∥AB,PQ∥AB,由AB∥CD,可得AB∥CD∥EF∥GH∥MN∥KL∥PQ,然后利用平行线的性质,即可证得∠2+∠4+∠6=∠1+∠3+∠5+∠7.
【考点精析】本题主要考查了平行线的性质的相关知识点,需要掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】在“一日捐”活动中,九(2)班42名同学捐款金额统计如下表,则在这次活动中,该班同学捐款金额的众数是( )
金额(元) | 20 | 30 | 35 | 50 | 100 | 150 |
学生数(名) | 5 | 7 | 9 | 13 | 5 | 3 |
A.3B.35C.50D.150
查看答案和解析>>
科目:初中数学 来源: 题型:
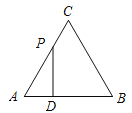
【题目】如图,△ABC是边长为4cm的等边三角形,动点P从点A出发,以2cm/s的速度沿A→C→B运动,到达B点即停止运动,PD⊥AB交AB于点D.设运动时间为x(s),△ADP的面积为y(cm2),则y与x的函数图象正确的是( )
A. 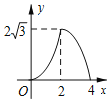 B.
B.  C.
C. 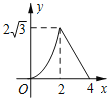 D.
D. 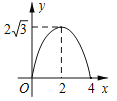
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com