
【题目】Rt△ABC中,∠ABC=90°,以AB为直径作⊙O交AC边于点D,E是边BC的中点,连接DE,OD.
(Ⅰ)如图①,求∠ODE的大小;
(Ⅱ)如图②,连接OC交DE于点F,若OF=CF,求∠A的大小.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】下列图案由边长相等的黑白两色正方形按一定规律拼接而成,观察图案回答问题:
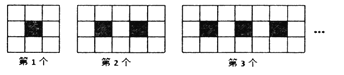
第![]() 个图案中白色正方形的个数为 .
个图案中白色正方形的个数为 .
第![]() 个图案中白色正方形的个数为 .
个图案中白色正方形的个数为 .
第![]() 个图案中白色正方形的个数有多少个?
个图案中白色正方形的个数有多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠A=90°, ∠B=30°,BC=![]() +1,点E、F分别是BC、AC边上的动点,沿EF所在直线折叠∠C,使点C的对应点C′始终落在边AB上,若△BEC′是直角三角形时,则BC′的长为_____________.
+1,点E、F分别是BC、AC边上的动点,沿EF所在直线折叠∠C,使点C的对应点C′始终落在边AB上,若△BEC′是直角三角形时,则BC′的长为_____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如果10b=n,那么称b为n的劳格数,记为b=d(n).
(1)根据劳格数的定义,可知:d(10)=1,d(102)=2,那么:d(103)= .
(2)劳格数有如下运算性质:若m,n为正数,则d(mn)=d(m)+d(n); d(![]() )=d(m)﹣d(n).若d(3)=0.48,d(2)=0.3,根据运算性质,填空:d(6)= ,则d(
)=d(m)﹣d(n).若d(3)=0.48,d(2)=0.3,根据运算性质,填空:d(6)= ,则d(![]() )= ,d(
)= ,d(![]() )= .
)= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(背景知识)
数轴是初中数学的一个重要工具.利用数轴可以将数与形完美的结合.研究数轴我们发现了许多重要的规律:数轴上A点、B点表示的数为a、b,则A,B两点之间的距离AB=|a-b|,若a>b,则可简化为AB=a-b;线段AB的中点M表示的数为![]() .
.
(问题情境)
已知数轴上有A、B两点,分别表示的数为-10,8,点A以每秒3个单位的速度沿数轴向右匀速运动,点B以每秒2个单位向左匀速运动.设运动时间为t秒(t>0).
![]()
(综合运用)
(1)运动开始前,A、B两点的距离为______;线段AB的中点M所表示的数______.
(2)点A运动t秒后所在位置的点表示的数为______;点B运动t秒后所在位置的点表示的数为______;(用含t的式子表示)
(3)它们按上述方式运动,A、B两点经过多少秒会相距4个单位长度?
(4)若A,B按上述方式运动,直接写出中点M的运动方向和运动速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工人计划加工一批产品,如果每小时加工产品10个,就可以在预定时间完成任务,如果每小时多加工2个,就可以提前1小时完成任务.
(1)该产品的预定加工时间为几小时?
(2)若该产品销售时的标价为100元/个,按标价的八折销售时,每个仍可以盈利25元,该批产品总成本为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点O是直线AB上一点,射线OD,OE分别是∠BOC,∠AOC的平分线.

(1)图中共有几对互余角?请写出来
(2)若∠AOE=31°,求∠AOC和∠DOC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
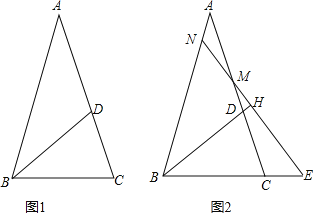
【题目】如图,在![]() 中,
中,![]() ,D在边AC上,且
,D在边AC上,且![]() .
.
![]() 如图1,填空
如图1,填空![]() ______
______![]() ,
,![]() ______
______![]()
![]() 如图2,若M为线段AC上的点,过M作直线
如图2,若M为线段AC上的点,过M作直线![]() 于H,分别交直线AB、BC与点N、E.
于H,分别交直线AB、BC与点N、E.
![]() 求证:
求证:![]() 是等腰三角形;
是等腰三角形;
![]() 试写出线段AN、CE、CD之间的数量关系,并加以证明.
试写出线段AN、CE、CD之间的数量关系,并加以证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com