
【题目】矩形![]() 与矩形
与矩形![]() 如图放置,点
如图放置,点![]() 共线,
共线,![]() 共线,连接
共线,连接![]() ,取
,取![]() 的中点
的中点![]() ,连接
,连接![]() ,若
,若![]() ,
,![]() ,则
,则![]() ( )
( )

A. ![]() B.
B. ![]() C. 2D.
C. 2D. ![]()
【答案】A
【解析】
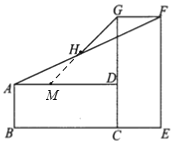
如图,延长GH交AD于点M,先证明△AHM≌△FHG,从而可得AM=FG=1,HM=HG,进而得DM=AD-AM=2,继而根据勾股定理求出GM的长即可求得答案.
如图,延长GH交AD于点M,
∵四边形ABCD、CEFG是矩形,
∴AD=BC=3,CG=EF=3,FG=CE=1,∠CGF=90°,∠ADC=90°,
∴DG=CG-CD=3-1=2,∠ADG=90°=∠CGF,
∴AD//FG,
∴∠HAM=∠HFG,∠AMH=∠FGH,
又AH=FH,
∴△AHM≌△FHG,
∴AM=FG=1,HM=HG,
∴DM=AD-AM=3-1=2,
∴GM=![]() ,
,
∵GM=HM+HG,
∴GH=![]() ,
,
故选A.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】先化简,再求值:
阅读材料,大数学家高斯在上学读书时曾经研究过这样一个问题:1+2+3+…+100=?经过研究,这个问题的一般性结论是1+2+3+…+![]() ,其中n是正整数。现在我们来研究一个类似的问题:1×2+2×3+…
,其中n是正整数。现在我们来研究一个类似的问题:1×2+2×3+…![]() =?
=?
观察下面三个特殊的等式
![]()
![]()
![]()
将这三个等式的两边相加,可以得到1×2+2×3+3×4=![]()
读完这段材料,请你思考后回答:(只需写出结果,不必写中间的过程)
(1)![]()
(2)1×2+2×3+3×4+…+n×(n+1)=
(3)![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在运动会径赛中,甲、乙同时起跑,刚跑出200m,甲不慎摔倒,他又迅速地爬起来继续投入比赛,若他们所跑的路程y(m)与比赛时间x(s)的关系如图,有下列说法:①他们进行的是800m比赛;②乙全程的平均速度为6.4m/s;③甲摔倒之前,乙的速度快;④甲再次投入比赛后的平均速度为7.5m/s;⑤甲再次投入比赛后在距离终点300米时追上了乙.其中正确的个数有( )
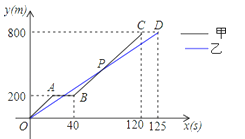
A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小张骑车往返于甲、乙两地,距甲地的路程y(千米)与时间x(时)的函数图象如图所示.
(1)小张在路上停留 小时,他从乙地返回时骑车的速度为 千米/时;
(2)小王与小张同时出发,按相同路线匀速前往乙地,距甲地的路程y(千米)与时间x(时)的函数关系式为y=10x+10.请作出此函数图象,并利用图象回答:小王与小张在途中共相遇 次;
(3)请你计算第三次相遇的时间.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在![]() 中,
中,![]() ,
,![]() ,把一块含
,把一块含![]() 角的三角板
角的三角板![]() 的直角顶点
的直角顶点![]() 放在
放在![]() 的中点上(直角三角板的短直角边为
的中点上(直角三角板的短直角边为![]() ,长直角边为
,长直角边为![]() ),点
),点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上.
上.
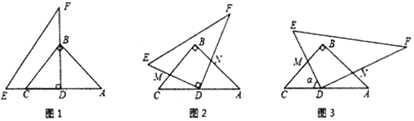
(1)求重叠部分![]() 的面积;
的面积;
(2)如图2,将直角三角板![]() 绕
绕![]() 点按顺时针方向旋转30度,
点按顺时针方向旋转30度,![]() 交
交![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() .
.
①请说明:![]() ;
;
②在此条件下,![]() 与直角三角板
与直角三角板![]() 重叠部分的面积会发生变化吗?请说明理由,并求出重叠部分的面积.
重叠部分的面积会发生变化吗?请说明理由,并求出重叠部分的面积.
(3)如图3,将直角三角板![]() 绕
绕![]() 点按顺时针方向旋转
点按顺时针方向旋转![]() 度(
度(![]() ),
),![]() 交
交![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,则
,则![]() 的结论仍成立吗?重叠部分的面积会变吗?(请直接写出结论,不需要说明理由)
的结论仍成立吗?重叠部分的面积会变吗?(请直接写出结论,不需要说明理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=﹣x2+bx+c经过A(﹣1,0),B(4,0)两点,与y轴相交于点C,连结BC,点P为抛物线上一动点,过点P作x轴的垂线l,交直线BC于点G,交x轴于点E.
(1)求抛物线的表达式;
(2)当P位于y轴右边的抛物线上运动时,过点C作CF⊥直线l,F为垂足,当点P运动到何处时,以P,C,F为顶点的三角形与△OBC相似?并求出此时点P的坐标;

(3)如图2,当点P在位于直线BC上方的抛物线上运动时,连结PC,PB,请问△PBC的面积S能否取得最大值?若能,请求出最大面积S,并求出此时点P的坐标,若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
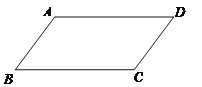
【题目】如图,已知AD∥BC,要使四边形ABCD为平行四边形,需要增加的一个条是:_____.(只填一个你认为正确的条件即可,不添加任何线段与字母)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:关于![]() 的两个一次二项式,其中任意一个式子的一次项系数都是另一个式子的常数项,则称这两个式子互为“田家炳式”.例如,式子
的两个一次二项式,其中任意一个式子的一次项系数都是另一个式子的常数项,则称这两个式子互为“田家炳式”.例如,式子![]() 与
与![]() 互为“田家炳式”.
互为“田家炳式”.
(1)判断式子![]() 与
与![]() ______(填“是”或“不是”)互为“田家炳式”;
______(填“是”或“不是”)互为“田家炳式”;
(2)已知式子![]() 的“田家炳式”是
的“田家炳式”是![]() 且数
且数![]() 、
、![]() 在数轴上所对应的点为
在数轴上所对应的点为![]() 、
、![]() .在数轴上有一点
.在数轴上有一点![]() 到
到![]() 、
、![]() 两点的距离的和
两点的距离的和![]() ,求点
,求点![]() 在数轴上所对应的数.
在数轴上所对应的数.
(3)在(2)的条件下,若![]() 点,
点,![]() 点同时沿数轴向正方向运动,
点同时沿数轴向正方向运动,![]() 点的速度是
点的速度是![]() 点速度的2倍,且3秒后,
点速度的2倍,且3秒后,![]() ,求点
,求点![]() 的速度.
的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在四边形ABCD中,∠A=∠C=90°.
(1)∠ABC+∠ADC= °;
(2)如图①,若DE平分∠ADC,BF平分∠ABC的外角,请写出DE与BF的位置关系,并证明;
(3)如图②,若BE,DE分别四等分∠ABC、∠ADC的外角(即∠CDE=![]() ∠CDN,∠CBE=
∠CDN,∠CBE=![]() ∠CBM),试求∠E的度数.
∠CBM),试求∠E的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com