
【题目】如图,在平面直角坐标系中,已知点A(0,2),△AOB为等边三角形,P是x轴上一个动点(不与原点O重合),以线段AP为一边在其右侧作等边三角形APQ.
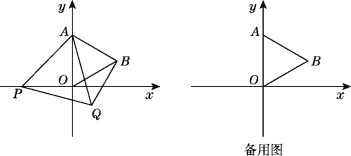
(1)求点B的坐标.
(2)在点P运动过程中,∠ABQ的大小是否发生改变?若不改变,求出其大小;若改变,请说明理由.
(3)连接OQ,当OQ∥AB时,求点P的坐标.
【答案】(1) 点B的坐标为(![]() ,1);(2)∠ABQ的大小始终不变,∠ABQ=90°;(3) P的坐标为(-
,1);(2)∠ABQ的大小始终不变,∠ABQ=90°;(3) P的坐标为(-![]() ,0)
,0)
【解析】
(1)过点B作BC⊥x轴于点C,根据等边三角形的性质可得∠AOB=60°,BO=OA=2,从而求出∠BOC=30°,然后根据30°所对的直角边是斜边的一半和勾股定理即可求出BC和OC,从而求出点B的坐标;
(2)根据等边三角形的性质可得AP=AQ,AO=AB,∠PAQ=∠OAB=60°,从而证出∠PAO=∠QAB,然后利用SAS证出△APO≌△AQB,从而得出∠ABQ=∠AOP=90°;
(3)根据题意,画出图形,然后根据平行线的性质可得∠BQO=90°,∠BOQ=∠ABO=60°,从而求出∠OBQ=30°,然后根据30°所对的直角边是斜边的一半和勾股定理即可求出OQ和BQ,再根据(2)中全等可得OP=BQ,从而求出点P的坐标.
解:(1)如图①,过点B作BC⊥x轴于点C.
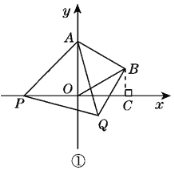
∵△AOB为等边三角形,且OA=2,
∴∠AOB=60°,BO=OA=2.
∴∠BOC=30°.
又∵∠OCB=90°,
∴BC=![]() OB=1,OC=
OB=1,OC=![]() .
.
∴点B的坐标为(![]() ,1).
,1).
(2)∠ABQ的大小始终不变.
∵△APQ,△AOB均为等边三角形,
∴AP=AQ,AO=AB,∠PAQ=∠OAB=60°.
∴∠PAO=∠QAB.
在△APO与△AQB中,
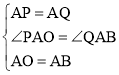
∴△APO≌△AQB(SAS).
∴∠ABQ=∠AOP=90°.
(3)如图②,当OQ∥AB时,点P在x轴的负半轴上,点Q在点B的下方,
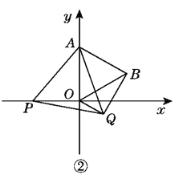
∵AB∥OQ,
∴∠BQO=180°-∠ABQ=90°,∠BOQ=∠ABO=60°.
∴∠OBQ=30°.
又OB=OA=2,
∴OQ=![]() OB=1,BQ=
OB=1,BQ=![]() ,
,
由(2)可知,△APO≌△AQB,
∴OP=BQ=![]() .
.
∴此时点P的坐标为(-![]() ,0).
,0).


科目:初中数学 来源: 题型:
【题目】在三个不透明的布袋中分别放入一些除颜色不同外其他都相同的玻璃球,并搅匀,具体情况如下表:

在下列事件中,哪些是随机事件,哪些是必然事件,哪些是不可能事件?
(1) 随机从第一个布袋中摸出一个玻璃球,该球是黄色、绿色或红色的;
(2) 随机的从第二个布袋中摸出两个玻璃球,两个球中至少有一个不是绿色的;
(3) 随机的从第三个布袋中摸出一个玻璃球,该球是红色的;
(4)随机的从第一个布袋中和第二个布袋中各摸出一个玻璃球,两个球的颜色一致.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】满足下列条件的△ABC不是直角三角形的是()
A. BC=1,AC=2,AB=![]()
B. BC=1,AC=2,AB=![]()
C. BC:AC:AB=3:4:5
D. ∠A:∠B:∠C=3:4:5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E是正方形ABCD的对角线BD上一点,并且AD=DE,过点E作EF⊥BD交AB于点F.
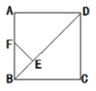
(1)求证:AF=BE,(2)若正方形的边长为1,求BF的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BP是∠ABC的平分线,AP⊥BP于P,连接PC,若△ABC的面积为1cm2则△PBC的面积为( ).
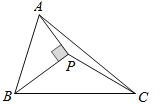
A. 0.4 cm2B. 0.5 cm2
C. 0.6 cm2D. 不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,D是AB上一点,E是BC延长线上一点,AD=CE,DE交AC于点F.
(1)求证:DF=EF;
(2)过点D作DH⊥AC于点H,求![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中的每个小方格都是边长为 1 个单位的正方形,Rt△ ABC 的顶点均在个点上,在建立平面直角坐标系后,点 A 的坐标为(﹣6,1),点 B 的坐标为(﹣3,1),点 C 的坐标为(﹣3,3).
(1)将 Rt△ABC沿 x 轴正方向平移5个单位得到 Rt△A1B1C1,试在图上画出的图形 Rt△A1B1C1,并写出点A1的坐标;
(2)将原来的 Rt△ABC 绕点 B 顺时针旋转 90°得到 Rt△A2B2C2,试在图上画出Rt△A2B2C2的图形.
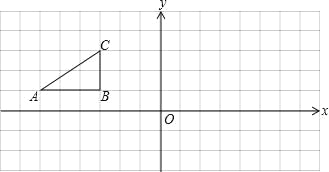
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】笑笑将一副三角板按如图所示的位置放置,△DOE的直角顶点O在边BC的中点处,其中∠A=∠DOE=90°.∠B=45°,∠D=60°,△DOE绕点O自由旋转,且OD,OE分别交AB,AC于点M,N当AN=4,NC=2时,MN的长为_____.
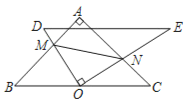
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com