练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

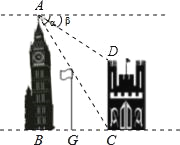
    【题目】如图，在两建筑物之间有一旗杆，高15米，从A点经过旗杆顶点恰好看到矮建筑物的墙角C点，且俯角α为60°，又从A点测得D点的俯角β为30°，若旗杆底点G为BC的中点，则矮建筑物的高CD为（ ）

    A. 20米 B. 米 C. 米 D. 米

    【答案】A

    【解析】

    根据点G是BC中点，可判断EG是△ABC的中位线，求出AB，在Rt△ABC中求出BC，在Rt△AFD中求出DF，继而可求出CD的长度．

    ∵点G是BC中点，EG∥AB，

    ∴EG是△ABC的中位线，

    ∴AB=2EG=30米，

    在Rt△ABC中，∠CAB=30°，

    则BC=ABtan∠BAC=30×=10米．

    如图，过点D作DF⊥AF于点F．

    在Rt△AFD中，AF=BC=10米，

    则FD=AFtanβ=10×=10米，

    综上可得：CD=AB-FD=30-10=20米．

    故选A．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

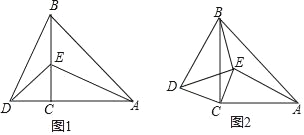
    【题目】△DCE和△ABC是一大一小两块等腰三角尺，∠DCE＝∠ACB＝90°，AC＝BC，EC＝DC．

    （1）如图1所示，若∠DBE＝28°，试求∠AEB的大小；

    （2）若将△DCE绕C点顺时针旋转到图2所示，∠DBE＝n°，试求∠AEB的大小．（用含n的式子表示）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

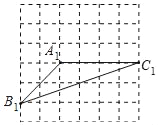
    【题目】如图是边长为1的正方形网格，△A1B1C1的顶点均在格点上．

    （1）在该网格中画出△A2B2C2（顶点均在格点上），使△A2B2C2∽△A1B1C1；

    （2）请写出（1）中作图的主要步骤，并说明△A2B2C2和△A1B1C1相似的依据．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知抛物线y=ax2+bx+c经过点A（-1，0），且经过直线y=x-2与x轴的交点B及与y轴的交点C．

    （1）求抛物线的解析式；

    （2）求抛物线的顶点坐标；

    （3）若点M在第四象限内的抛物线上，且tan∠MOC=1，求M点的坐标及四边形OBMC面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小明想测量一棵树的高度，他发现树的影子恰好落在地面和一斜坡上；如图，此时测得地面上的影长为8米，坡面上的影长为4米．已知斜坡的坡角为30°，同一时刻，一根长为1米，垂直于地面放置的标杆在地面上的影长为2米，则树的高度为___．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

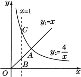
    【题目】函数y1=x(x≥0),y2=(x>0)的图象如图所示,下列结论:

    ①两函数图象的交点坐标为A(2,2);

    ②当x>2时,y2>y1;

    ③直线x=1分别与两个函数图象相交于B,C两点,则线段BC的长为3;

    ④当x逐渐增大时,y1的值随x的增大而增大,y2的值随x的增大而减少,其中正确的是(　　)

    A. ①② B. ①③ C. ②④ D. ①③④

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了预防流感，某学校在休息天用药薰消毒法对教室进行消毒.已知药物释放过程中，室内每立方米空气中含药量y（毫克）与时间x（分钟）成正比例；药物释放完毕后，y与x成反比例，如图所示.根据图中提供的信息，解答下列问题：

    （1）写出从药物释放开始，y与x之间的两个函数关系式及相应的自变量取值范围；

    （2）据测定，当空气中每立方米的含药量降低到0.45毫克以下时，学生方可进入教室，那么从药物释放开始，至少需要经过多少小时后，学生才能进入教室？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AB是⊙O的直径，弦CD⊥AB于点E，AM是△ACD的外角∠DAF的平分线．

    （1）求证：AM是⊙O的切线；

    （2）若∠D = 60°，AD = 2，射线CO与AM交于N点，请写出求ON长的思路．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，则下列结论：①ab＞0；②a+3b+9c＞0；③4a+b=0；④当y=﹣2时，x的值只能为0；⑤3b﹣c＜0，其中正确的个数是（　　）

    A. 1个 B. 2个 C. 3个 D. 4个

    查看答案和解析>>

    同步练习册答案