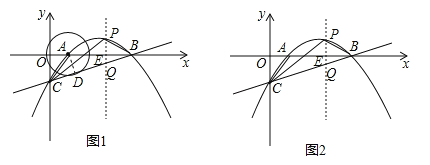
【题目】如图，抛物线经过点A（1，0）和点B（5，0），与y轴交于点C．

（1）求抛物线的解析式；

（2）以点A为圆心，作与直线BC相切的⊙A，请判断⊙A与y轴有怎样的位置关系，并说明理由；

（3）在直线BC上方的抛物线上任取一点P，连接PB、PC，请问：△PBC的面积是否存在最大值？若存在，求出这个值和此时点P的坐标；若不存在，请说明理由．

参考答案：

【答案】（1）；（2）相交；（3）S△PBC有最大值，此时P点坐标为（，）．

【解析】

试题分析：（1）把A、B两点分别代入抛物线解析可求得a和b，可求得抛物线解析式；

（2）过A作AD⊥BC于点D，则AD为⊙A的半径，由条件可证明△ABD∽△CBO，利用相似三角形的性质可求得AD的长，可求得半径，进而得出答案；

（3）由待定系数法可求得直线BC解析式，过P作PQ∥y轴，交直线BC于点Q，交x轴于点E，可设出P、Q的坐标，可表示出△PQC和△PQB的面积，可表示出△PBC的面积，再利用二次函数的性质可求得其最大值，容易求得P点坐标．

试题解析：（1）∵抛物线经过点A（1，0）和点B（5，0），∴把A、B两点坐标代入可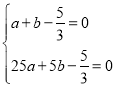得，解得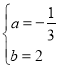：，∴抛物线解析式为；

（2）相交，理由：过A作AD⊥BC于点D，如图1，∵⊙A与BC相切，∴AD为⊙A的半径，由（1）可知C（0，﹣），且A（1，0），B（5，0），∴OB=5，AB=OB﹣OA=4，OC=，在Rt△OBC中，由勾股定理可得BC===，∵∠ADB=∠BOC=90°，∠ABD=∠CBO，∴△ABD∽△CBO，∴，即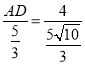，解得AD=，即⊙A的半径为，∵＞1，∴⊙A与y轴相交；

（3）∵C（0，﹣），∴可设直线BC解析式为y=kx﹣，把B点坐标代入可求得k=，∴直线BC的解析式为，过P作PQ∥y轴，交直线BC于点Q，交x轴于点E，如图2，设P（x，），则Q（x，），∴PQ=（）﹣（）= =，∴S△PBC=S△PCQ+S△PBQ=PQOE+PQBE=PQ（OE+BE）=PQOB=PQ=，∴当x=时，S△PBC有最大值，此时P点坐标为（，），∴当P点坐标为（，）时，△PBC的面积有最大值．

关闭