Question

7．如图，在平面直角坐标系中，二次函数y=x²+bx+c的图象与x轴交于A、B两点，A点在原点的左侧，B点的坐标为（3，0），与y轴交于C（0，-3）点，点P是直线BC下方的抛物线上一动点．
（1）求这个二次函数的表达式；
（2）当点P运动到什么位置时，△BPC的面积最大？求出此时P点的坐标和△BPC的最大面积；
（3）连接PO、PC，并把△POC沿CO翻折，得到四边形POP₁C，那么是否存在点P，使四边形POP₁C为菱形？若存在，直接写出此时点P的坐标；若不存在，请说明理由．

Answer 1

分析 （1）直接把B（3，0）、C（0，-3）代入y=x²+bx+c可得到关于b、c的方程组，解方程组求得b=-2，c=-3，则二次函数的表达式为y=x²-2x-3；
（2）根据平行于y轴的直线上两点间的距离是较大的纵坐标减较小的纵坐标，可得P′E的长，根据面积的和差，可得二次函数，根据二次函数的性质，可得答案；
（3）作OC的垂直平分线交直线BC下方的抛物线于点P，则PO=PC，根据翻折的性质得OP′=OP，CP′=CP，易得四边形POP′C为菱形，又E点坐标为（0，-$\frac{3}{2}$），则点P的纵坐标为-$\frac{3}{2}$，再把y=-$\frac{3}{2}$代入y=x²-2x-3可求出对应x的值，然后确定满足条件的P点坐标．

解答 解：（1）把B（3，0）、C（0，-3）代入y=x²+bx+c，得
$\left\{\begin{array}{l}{9+3b+c=0}\\{c=-3}\end{array}\right.$，解得 $\left\{\begin{array}{l}{b=-2}\\{c=-3}\end{array}\right.$，
∴这个二次函数的表达式为y=x²-2x-3；
（2）如图1，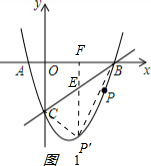
作PF⊥x轴于F点，交BC于E点，
BC的解析式为y=x-3，设E（m，m-3），P′（m，m²-2m-3）．
P′E=m-3-（m²-2m-3）=-m²+3m=-（m-$\frac{3}{2}$）²+$\frac{9}{4}$，
S_△BCP′=S_△BEP′+S_CEP′=$\frac{1}{2}$P′E×FB+$\frac{1}{2}$EP′•OF
=$\frac{1}{2}$EP′•OB
=$\frac{1}{2}$×3[-（m-$\frac{3}{2}$）²+$\frac{9}{4}$]
当m=$\frac{3}{2}$时，S_最大=$\frac{1}{2}$×3×$\frac{9}{4}$=$\frac{27}{8}$，
m²-2m-3=-$\frac{15}{4}$，
此时P′（$\frac{3}{2}$，-$\frac{15}{4}$）；
（3）存在．理由如下：
作OC的垂直平分线交直线BC下方的抛物线于点P，垂足为点E，如图2，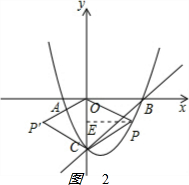
则PO=PC，
∵△POC沿CO翻折，得到四边形POP′C，
∴OP′=OP，CP′=CP，
∴OP′=OP=CP′=CP，
∴四边形POP′C为菱形，
∵C点坐标为（0，-3），
∴E点坐标为（0，-$\frac{3}{2}$），
∴点P的纵坐标为-$\frac{3}{2}$，
把y=-$\frac{3}{2}$代入y=x²-2x-3得x²-2x-3=-$\frac{3}{2}$，
解得x=$\frac{2±\sqrt{10}}{2}$，
∵点P在直线BC下方的抛物线上，
∴x=$\frac{2+\sqrt{10}}{2}$，
∴满足条件的点P的坐标为（ $\frac{2+\sqrt{10}}{2}$，-$\frac{3}{2}$）．

点评 本题考查了二次函数综合题：二次函数y=ax²+bx+c（a、b、c为常数，a≠0）的图象为抛物线，其顶点式为y=a（x-$\frac{b}{2a}$）²+$\frac{4ac-{b}^{2}}{4a}$，抛物线的对称轴为x=-$\frac{b}{2a}$，当a＞0，y_最小值=$\frac{4ac-{b}^{2}}{4a}$；当a＜0，y_最，大值=$\frac{4ac-{b}^{2}}{4a}$；利用面积的和差得出二次函数是解题关键，又利用了二次函数的性质；对于特殊四边形的判定与性质以及勾股定理要熟练运用．