
【题目】如图1,抛物线y=﹣ ![]() x2+
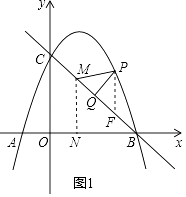
x2+ ![]() x+2的图象与x轴交于点A、B,与y轴交于点C,连接BC,过点A作AD∥BC交抛物线的对称轴于点D.
x+2的图象与x轴交于点A、B,与y轴交于点C,连接BC,过点A作AD∥BC交抛物线的对称轴于点D.

(1)求点D的坐标;
(2)如图2,点P是抛物线在第一象限内的一点,作PQ⊥BC于Q,当PQ的长度最大时,在线段BC上找一点M(不与点B、点C重合),使PM+ ![]() BM的值最小,求点M的坐标及PM+
BM的值最小,求点M的坐标及PM+ ![]() BM的最小值;
BM的最小值;
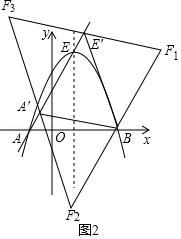
(3)抛物线的顶点为点E,平移抛物线,使抛物线的顶点E在直线AE上移动,点A,E平移后的对应点分别为点A′、E′.在平面内有一动点F,当以点A′、E′、B、F为顶点的四边形为菱形时,求出点A′的坐标.
【答案】
(1)
解:当y=0时,﹣ ![]() x2+
x2+ ![]() x+2=0,
x+2=0,
解得x1= ![]() ,x2=﹣
,x2=﹣ ![]() ,
,
即A(﹣ ![]() ,0),B(
,0),B( ![]() ,0),
,0),
当x=0时,y=2,即C(0,2),
直线BC的解析式为y=﹣ ![]() x+2,
x+2,
直线AD的解析式为y=﹣ ![]() x﹣
x﹣ ![]() ,
,
抛物线的对称轴为x=﹣ ![]() =
= ![]() ,
,
当x= ![]() 时,y=﹣
时,y=﹣ ![]() x﹣
x﹣ ![]() =﹣
=﹣ ![]() ,
,
即D点坐标为( ![]() ,﹣
,﹣ ![]() )
)
(2)
解:如图1,作PF∥y轴交BC于F,
则△PQF∽△BOC,
∴ ![]() =
= ![]() =
= ![]()
即PQ= ![]() PF
PF
设P(t,﹣ ![]() t2+
t2+ ![]() t+2),F(t,
t+2),F(t, ![]() t+2)
t+2)
∴PF=﹣ ![]() t2+
t2+ ![]() t
t
当t= ![]() 时,PF取最大值,PQ取最大值,
时,PF取最大值,PQ取最大值,
此时P( ![]() ,
, ![]() )
)
作MN⊥x轴于N,则△BMN∽△BOC,
∴ ![]() =
= ![]() =
= ![]()
即MN= ![]() BM,
BM,
则当P,M,N共线时,PM+ ![]() BM=PN=
BM=PN= ![]() ,
,
M( ![]() ,1)
,1)
(3)
解:如图2所示,
1)当A′E′=A′B,A′E′∥BF1,A′E′=BF1时四边形A′E′F1B是菱形,
此时A1′( ![]() ,
, ![]() ),A2′(﹣
),A2′(﹣ ![]() ,﹣
,﹣ ![]() );
);
2)当A′E′=E′B,A′E′∥BF2,A′E′=BF2时四边形A′E′F2B是菱形,
此时A3′(﹣ ![]() ,0),A4′(﹣
,0),A4′(﹣ ![]() ,﹣
,﹣ ![]() );
);
3)当A′B=E′B,A′F3∥BE′,A′F3=BE′时四边形A′F3E′B是菱形,
此时A5′(﹣ ![]() ,﹣
,﹣ ![]() ).
).
【解析】(1)当y=0时,﹣ ![]() x2+
x2+ ![]() x+2=0,解方程可得A(﹣
x+2=0,解方程可得A(﹣ ![]() ,0),B(
,0),B( ![]() ,0),当x=0时,y=2,即C(0,2),根据待定系数法可求直线BC的解析式为y=
,0),当x=0时,y=2,即C(0,2),根据待定系数法可求直线BC的解析式为y= ![]() x+2,根据平行两直线间的关系可得直线AD的解析式为y=﹣
x+2,根据平行两直线间的关系可得直线AD的解析式为y=﹣ ![]() x﹣
x﹣ ![]() ,根据抛物线的对称轴为x=﹣
,根据抛物线的对称轴为x=﹣ ![]() =
= ![]() ,可得当x=
,可得当x= ![]() 时,y=﹣
时,y=﹣ ![]() x﹣
x﹣ ![]() =﹣
=﹣ ![]() ,即D点坐标为(
,即D点坐标为( ![]() ,﹣
,﹣ ![]() );(2)如图1,作PF∥y轴交BC于F,则△PQF∽△BOC,根据相似三角形的性质可得PQ=
);(2)如图1,作PF∥y轴交BC于F,则△PQF∽△BOC,根据相似三角形的性质可得PQ= ![]() PF,设P(t,﹣
PF,设P(t,﹣ ![]() t2+
t2+ ![]() t+2),F(t,
t+2),F(t, ![]() t+2)可得PF=﹣
t+2)可得PF=﹣ ![]() t2+
t2+ ![]() t,当t=
t,当t= ![]() 时,PF取最大值,PQ取最大值,此时P(
时,PF取最大值,PQ取最大值,此时P( ![]() ,
, ![]() ),作MN⊥x轴于N,则△BMN∽△BOC,根据相似三角形的性质可得MN=
),作MN⊥x轴于N,则△BMN∽△BOC,根据相似三角形的性质可得MN= ![]() BM,则当P,M,N共线时,PM+
BM,则当P,M,N共线时,PM+ ![]() BM=PN=
BM=PN= ![]() ,M(
,M( ![]() ,1)(3)如图2所示,分三种情况:1)当A′E′=A′B,A′E′∥BF1 , A′E′=BF1时四边形A′E′F1B是菱形;2)当A′E′=E′B,A′E′∥BF2 , A′E′=BF2时四边形A′E′F2B是菱形;3)当A′B=E′B,A′F3∥BE′,A′F3=BE′时四边形A′F3E′B是菱形;进行讨论即可求解.
,1)(3)如图2所示,分三种情况:1)当A′E′=A′B,A′E′∥BF1 , A′E′=BF1时四边形A′E′F1B是菱形;2)当A′E′=E′B,A′E′∥BF2 , A′E′=BF2时四边形A′E′F2B是菱形;3)当A′B=E′B,A′F3∥BE′,A′F3=BE′时四边形A′F3E′B是菱形;进行讨论即可求解.
【考点精析】利用二次函数的图象和二次函数的性质对题目进行判断即可得到答案,需要熟知二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.


科目:初中数学 来源: 题型:
【题目】如图所示,体育场内一看台与地面所成夹角为30°,看台最低点A到最高点B的距离为10![]() ,A,B两点正前方有垂直于地面的旗杆DE.在A,B两点处用仪器测量旗杆顶端E的仰角分别为60°和15°(仰角即视线与水平线的夹角)
,A,B两点正前方有垂直于地面的旗杆DE.在A,B两点处用仪器测量旗杆顶端E的仰角分别为60°和15°(仰角即视线与水平线的夹角)
(1)
求AE的长;
(2)已知旗杆上有一面旗在离地1米的F点处,这面旗以0.5米/秒的速度匀速上升,求这面旗到达旗杆顶端需要多少秒?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点P在AD上,且不与A、D重合,BP的垂直平分线分别交CD、AB于E、F两点,垂足为Q,过E作EH⊥AB于H.
(1)求证:HF=AP;
(2)若正方形ABCD的边长为12,AP=4,求线段EQ的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC中,CA=CB,点O在高CH上,OD⊥CA于点D,OE⊥CB于点E,以O为圆心,OD为半径作⊙O. 
(1)求证:⊙O与CB相切于点E;
(2)如图2,若⊙O 过点H,且AC=5,AB=6,连结EH,求△BHE的面积. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解某校初三学生体能水平,体育老师从刚结束的“女生800米,男生1000米”体能测试成绩中随机抽取了一部分同学的成绩,按照“优秀、良好、合格、不合格”进行了统计,并绘制了下列不完整的统计图,
请根据图中信息解答下列问题:
(1)体育老师总共选取了多少人的成绩?扇形统计图中“优秀”部分的圆心角度数是多少?
(2)把条形统计图补充完整;
(3)已知某校初三在校生有2500人,从统计情况分析,请你估算此次体能测试中达到“优秀”水平的大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD中,E是AD的中点,连接CE并延长,与BA的延长线交于点F. 请你找出图中与AF相等的一条线段,并加以证明.(不再添加其它线段,不再标注或使用其它字母) 
(1)结论:AF= .
(2)证明结论。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,AC=5cm,BC=12cm,∠ACB=90°,把Rt△ABC所在的直线旋转一周得到一个几何体,则这个几何体的侧面积为( ) ![]()
A.60πcm2
B.65πcm2
C.120πcm2
D.130πcm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某校教学楼AB后方有一斜坡,已知斜坡CD的长为12米,坡角α为60°,根据有关部门的规定,∠α≤39°时,才能避免滑坡危险,学校为了消除安全隐患,决定对斜坡CD进行改造,在保持坡脚C不动的情况下,学校至少要把坡顶D向后水平移动多少米才能保证教学楼的安全?(结果取整数)
(参考数据:sin39°≈0.63,cos39°≈0.78,tan39°≈0.81, ![]() ≈1.41,
≈1.41, ![]() ≈1.73,
≈1.73, ![]() ≈2.24)
≈2.24)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com