

分析 (1)利用同角的余角相等得出∠GDA=∠EDC,进而得出△AGD≌△CED即可‘
(2)先判断出Rt△DRE≌Rt△DQG得出DR=DQ,进而判断出Rt△DRH≌Rt△DQH即可得出结论;
(3)方法一、利用三角函数求出DM=$\frac{4}{3}$,即可得出AM=$\frac{8}{3}$.再用勾股定理得出CM=$\frac{3\sqrt{10}}{3}$,最后用勾股定理即可得出结论;
方法二、利用四边形ACDG的面积直接计算即可得出结论.
解答 解:(1)AG=CE与AG⊥CE均成立.
∵四边形ABCD、四边形DEFG是正方形,
∴GD=DE,AD=DC
∵∠GDE=∠ADC=90°,
∴∠GDA=90°-∠ADE=∠EDC.
在△AGD和△CED中,$\left\{\begin{array}{l}{GD=DE}\\{∠GDA=∠EDC}\\{AD=DC}\end{array}\right.$,
∴△AGD≌△CED
∴AG=CE
∴∠GAD=∠ECD
又∵∠HMA=∠DMC.
∴∠AHM=∠ADC=90°.即AG⊥CE
(2)如图2,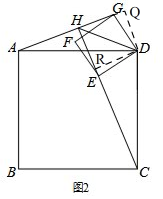 过D作DR⊥HC于R,DQ⊥AG于Q,
过D作DR⊥HC于R,DQ⊥AG于Q,
由(1)知,△AGD≌△CED,
∴∠DEC=∠DGA
∴∠DER=∠DGQ
在Rt△DRE和Rt△DQG中,$\left\{\begin{array}{l}{∠DRE=∠DQG}\\{∠DER=∠DGQ}\\{DE=DQ}\end{array}\right.$
∴Rt△DRE≌Rt△DQG
∴DR=DQ
在Rt△DRH和Rt△DQH中,
∵DR=DQ,DH=DH,∠DRH=∠DQH=90°
∴Rt△DRH≌Rt△DQH
∴∠DHR=∠DHQ
由(1)得AG⊥CE∴∠DHQ=45°.
(3)解法一:如图3,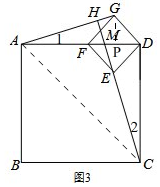 过G作GP⊥AD于P,
过G作GP⊥AD于P,
由题意有,GP=PD=$\sqrt{2}$sin45°=1,
∴AP=3,则tan∠1=$\frac{GP}{AP}=\frac{1}{3}$
而∠1=∠2,
∴tan∠2=$\frac{DM}{DC}$=tan∠1=$\frac{1}{3}$.
∴DM=$\frac{4}{3}$,即AM=AD-DM=$\frac{8}{3}$.
在Rt△DMC中,CM=$\sqrt{C{D}^{2}+D{M}^{2}}$=$\frac{3\sqrt{10}}{3}$,
而△AMH∽△CMD,
∴$\frac{AH}{DC}=\frac{AM}{CM}$,即$\frac{AH}{4}=\frac{\frac{8}{3}}{\frac{4\sqrt{10}}{3}}$,
∴AH=$\frac{4\sqrt{10}}{5}$;
连接AC,显然有AC=4$\sqrt{2}$,
∴CH=$\sqrt{A{C}^{2}-A{H}^{2}}$=$\frac{8\sqrt{10}}{5}$.
所求CH的长为$\frac{8\sqrt{10}}{5}$
解法二:研究四边形ACDG的面积
过G作GP⊥AD于P,由题意有GP=PD=$\sqrt{2}$sin45°=1,
∴AP=3,AG=$\sqrt{10}$
而以CD为底边的三角形CDG的高=PD=1,
S△AGD+S△ACD=S四边形ACDG=S△ACG+S△CGD,
∴4×1+4×4=$\sqrt{10}$×CH+4×1.
∴CH=$\frac{8\sqrt{10}}{5}$.
点评 此题是四边形综合题,主要考查了正方形的性质,全等三角形的判定和性质,勾股定理,锐角三角函数,四边形的面积的计算方法,解(2)的关键是判断出Rt△DRE≌Rt△DQG,解(3)的关键是求出CM=$\frac{3\sqrt{10}}{3}$.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
 如图ABC中,AB=AC,⊙O为△ABC的外接围,D为⊙O外一点,∠DCA=∠ACB.
如图ABC中,AB=AC,⊙O为△ABC的外接围,D为⊙O外一点,∠DCA=∠ACB.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 6x6÷2x2=3x2 | B. | 8x8÷4x2=2x6 | C. | a3÷a3=0 | D. | $\frac{2}{3}$a5b÷$\frac{3}{2}$a5b=1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
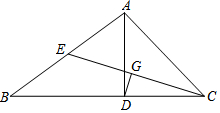 已知:如图,在△ABC中,AD是BC边上的高,∠B=30°,∠ACB=45°,CE是AB边上的中线.
已知:如图,在△ABC中,AD是BC边上的高,∠B=30°,∠ACB=45°,CE是AB边上的中线.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
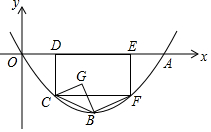 如图,在平面直角坐标系中,抛物线y=$\frac{1}{2}$ax2-2ax(a>0)与x轴正半轴交于点A,点B是抛物线的顶点,矩形CDEF的顶点D、E在x正半轴上,C、F在抛物线上,且点D的横坐标为1,连结BC、BF,以BC为斜边向右侧作等腰直角三角形BCG
如图,在平面直角坐标系中,抛物线y=$\frac{1}{2}$ax2-2ax(a>0)与x轴正半轴交于点A,点B是抛物线的顶点,矩形CDEF的顶点D、E在x正半轴上,C、F在抛物线上,且点D的横坐标为1,连结BC、BF,以BC为斜边向右侧作等腰直角三角形BCG查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com