
【题目】如图①,直线![]() 与反比例函数
与反比例函数![]() 的图象交于
的图象交于![]() ,
,![]() 两点,
两点,![]() 轴(点
轴(点![]() 在点
在点![]() 的右侧),且
的右侧),且![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,交反比例函数图象于点
,交反比例函数图象于点![]() .
.
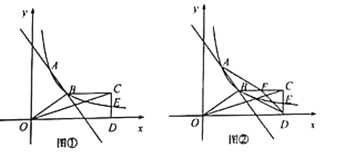
(1)求![]() 的值和反比例函数的解析式;
的值和反比例函数的解析式;
(2)填空:不等式![]() 的解集为______;
的解集为______;
(3)当![]() 平分
平分![]() 时,求
时,求![]() 的值;
的值;
(4)如图②,取![]() 中点
中点![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,当四边形
,当四边形![]() 为平行四边形时,求点
为平行四边形时,求点![]() 的坐标.
的坐标.
【答案】(1) ![]() ;(2)
;(2) ![]() ;(3)
;(3) ![]() ;(4)
;(4) ![]()
【解析】
(1) 将![]() 代入
代入![]() 可求出b的值,将
可求出b的值,将![]() 代入
代入![]() ,可求得反比例函数的表达式;
,可求得反比例函数的表达式;
(2)在第一象限内,根据A、B坐标写出一次函数图象在反比例函数图象上上方所对应的自变量的范围即可;
(3)求出B点坐标,得出![]() 及
及![]() ,由
,由 ![]() 平分
平分![]() ,可得
,可得![]() ,由
,由![]() 轴,可推
轴,可推![]() ,可得
,可得![]() =5,可得
=5,可得![]() ,及
,及 ![]() ,
,![]() .可得
.可得![]() ,
,![]() ,代入
,代入![]() 即可.
即可.
(4)作![]() 交于点
交于点![]() ,则
,则![]() ,可得
,可得![]() ,
,![]() ,由平行四边形的性质可得
,由平行四边形的性质可得![]() ,
,![]() ,故
,故![]() ,可证
,可证![]() ,得到
,得到![]() ,由于
,由于![]() 为
为![]() 中点,故
中点,故![]() ,可得
,可得![]() .
.
(1)将![]() 代入
代入![]() 得:
得:![]() ,解得:
,解得:![]() ,
,
将![]() 代入
代入![]() 得:
得:![]() ,
,
∴反比例函数的表达式为![]() .
.
(2)当y=3时![]() ,解得:x=4
,解得:x=4
∴B(4,3)
由图像可知不等式![]() 的解集为
的解集为![]() .
.
故答案为:![]()
(3)将![]() 代入
代入![]() 得:
得:![]() ,解得:
,解得:![]() ,
,
∵![]() 平分
平分![]() ,
,
∴![]() ,
,
∵![]() 轴,
轴,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() .
.
∴![]() ,
,![]() ,
,
∴![]() .
.
(4)作![]() 交于点
交于点![]() ,则
,则![]() .
.
∴![]() ,
,![]() ,
,
∵四边形![]() 为平行四边形,
为平行四边形,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() 为
为![]() 中点,
中点,
∴![]() ,
,
∵![]() ,
,
∴![]() .
.


科目:初中数学 来源: 题型:
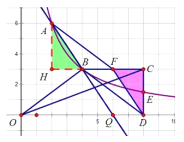
【题目】 一艘观光游船从港口A以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东37°方向,马上以40海里每小时的速度前往救援,求海警船到大事故船C处所需的大约时间.(温馨提示:sin53°≈0.8,cos53°≈0.6)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线![]() 经过点A,作AB⊥x轴于点B,将△ABO绕点B逆时针旋转60°得到△CBD.若点B的坐标为(2, 0),则点C的坐标为( )
经过点A,作AB⊥x轴于点B,将△ABO绕点B逆时针旋转60°得到△CBD.若点B的坐标为(2, 0),则点C的坐标为( )

A.(﹣1,![]() )B.(﹣2,
)B.(﹣2,![]() )C.(
)C.(![]() ,1)D.(
,1)D.(![]() ,2)
,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y1=2x2与坐标轴交于A、B两点,与双曲线y2=![]() (x>0)交于点C,过点C作CD⊥x轴,且OA=AD,则以下结论错误的是( )
(x>0)交于点C,过点C作CD⊥x轴,且OA=AD,则以下结论错误的是( )

A. 当x>0时,y1随x的增大而增大,y2随x的增大而减小;
B. k=4
C. 当0<x<2时,y1<y2
D. 当x=4时,EF=4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知直线y=x+3与x轴交于点A,与y轴交于点B,将直线在x轴下方的部分沿x轴翻折,得到一个新函数的图象(图中的“V形折线”).

(1)类比研究函数图象的方法,请列举新函数的两条性质,并求新函数的解析式;
(2)如图2,双曲线y=![]() 与新函数的图象交于点C(1,a),点D是线段AC上一动点(不包括端点),过点D作x轴的平行线,与新函数图象交于另一点E,与双曲线交于点P.
与新函数的图象交于点C(1,a),点D是线段AC上一动点(不包括端点),过点D作x轴的平行线,与新函数图象交于另一点E,与双曲线交于点P.
①试求△PAD的面积的最大值;
②探索:在点D运动的过程中,四边形PAEC能否为平行四边形?若能,求出此时点D的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
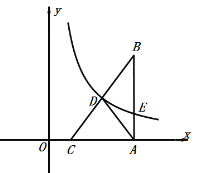
【题目】如图,在平面直角坐标系中,Rt△ABC的边AB⊥x轴,垂足为A,C的坐标为(1,0),反比例函数y=![]() (x>0)的图象经过BC的中点D,交AB于点E.已知AB=4,BC=5.求k的值
(x>0)的图象经过BC的中点D,交AB于点E.已知AB=4,BC=5.求k的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图以△ABC的一边AB为直径作⊙O,⊙O与BC边的交点D恰好为BC的中点,过点D作⊙O的切线交AC边于点F.

(1)求证:DF⊥AC;
(2)若∠ABC=30°,求tan∠BCO的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,![]() 是等边三角形,AP、BP的延长线分别交边CD于点E、F,联结AC、CP、AC与BF相交于点H,下列结论中错误的是( )
是等边三角形,AP、BP的延长线分别交边CD于点E、F,联结AC、CP、AC与BF相交于点H,下列结论中错误的是( )

A.AE=2DEB.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小组做“用频率估计概率”的实验时,统计了某一结果出现的频率,绘制了如图的折线统计图,则符合这一结果的实验最有可能的是( )
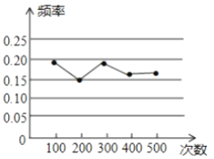
A.在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”
B.一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是红桃
C.暗箱中有1个红球和2个黄球,它们只有颜色上的区别,从中任取一球是黄球
D.掷一个质地均匀的正六面体骰子,向上的面点数是4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com