
【题目】如图,在正方形ABCD中,![]() 是等边三角形,AP、BP的延长线分别交边CD于点E、F,联结AC、CP、AC与BF相交于点H,下列结论中错误的是( )
是等边三角形,AP、BP的延长线分别交边CD于点E、F,联结AC、CP、AC与BF相交于点H,下列结论中错误的是( )

A.AE=2DEB.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
A.利用直角三角形30度角的性质即可解决问题.
B.根据两角相等两个三角形相似即可判断.
C.通过计算证明∠DPB≠∠DPF,即可判断.
D.利用相似三角形的性质即可证明.
解:∵四边形ABCD是正方形,
∴∠D=∠DAB=90°,
∵△ABP是等边三角形,
∴∠PAB=∠PBA=∠APB=60°,
∴∠DAE=30°,
∴AE=2DE,故A正确;
∵AB∥CD,
∴∠CFP=∠ABP=∠APH=60°,
∵∠PHA=∠PBA+∠BAH=60°+45°=105°,
又∵BC=BP,∠PBC=30°,
∴∠BPC=∠BCP=75°,
∴∠CPF=105°,
∴∠PHA=∠CPF,又易得∠APB=∠CFP=60°,
∴△CFP∽△APH,故B正确;
∵∠CPB=60°+75°=135°≠∠DPF,
∴△PFC与△PCA不相似,故C错误;
∵∠PCH=∠PCB-∠BCH=75°-45°=30°,
∴∠PCH=∠PBC,
∵∠CPH=∠BPC,
∴△PCH∽△PBC,
∴![]() ,
,
∴PC2=PHPB,故D正确,
故选:C.


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:初中数学 来源: 题型:
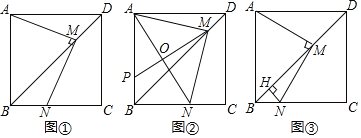
【题目】如图,在正方形![]() 中,
中,![]() 是对角线
是对角线![]() 上的一个动点
上的一个动点![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() .
.
(1)如图①,求证:![]() ;
;
(2)如图②,连接![]() 为
为![]() 的中点,
的中点,![]() 的延长线交边
的延长线交边![]() 于点
于点![]() ,当
,当![]() 时,求
时,求![]() 和
和![]() 的长;
的长;
(3)如图③,过点![]() 作
作![]() 于
于![]() ,当
,当![]() 时,求
时,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,直线![]() 与反比例函数
与反比例函数![]() 的图象交于
的图象交于![]() ,
,![]() 两点,
两点,![]() 轴(点
轴(点![]() 在点
在点![]() 的右侧),且
的右侧),且![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,交反比例函数图象于点
,交反比例函数图象于点![]() .
.
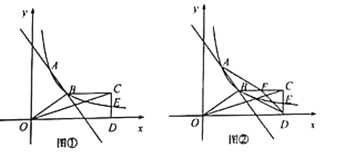
(1)求![]() 的值和反比例函数的解析式;
的值和反比例函数的解析式;
(2)填空:不等式![]() 的解集为______;
的解集为______;
(3)当![]() 平分
平分![]() 时,求
时,求![]() 的值;
的值;
(4)如图②,取![]() 中点
中点![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,当四边形
,当四边形![]() 为平行四边形时,求点
为平行四边形时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,PA、PB分别切圆O于A、B两点,C为劣弧AB上一点,∠APB=40°,则∠ACB=( ).
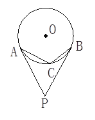
A.70°B.80°C.110°D.140°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有A、B两个黑布袋,A布袋中有四个除标号外完全相同的小球,小球上分别标有数字0,1,2,3,B布袋中有三个除标号外完全相同的小球,小球上分别标有数字0,1,2.小明先从A布袋中随机取出一个小球,用m表示取出的球上标有的数字,再从B布袋中随机取出一个小球,用n表示取出的球上标有的数字.
(1)若用(m,n)表示小明取球时m与n 的对应值,用列表法(或画树状图)表示出(m,n)的所有取值;
(2)求关于x的一元二次方程![]() 有实数根的概率.
有实数根的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
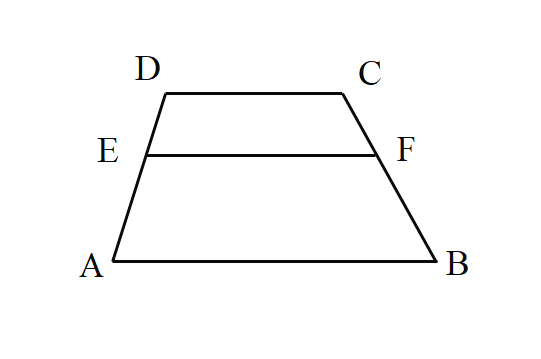
【题目】如图,已知在梯形ABCD中,AB//CD,AB=12,CD=7,点E在边AD上,![]() ,过点E作EF//AB交边BC于点F.
,过点E作EF//AB交边BC于点F.
(1)求线段EF的长;
(2)设![]() ,
,![]() ,联结AF,请用向量
,联结AF,请用向量![]() 表示向量
表示向量![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
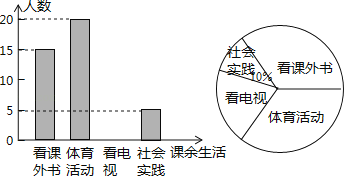
【题目】为了解某中学学生课余生活情况,对喜爱看课外书、体育活动、看电视、社会实践四个方面的人数进行调查统计.现从该校随机抽取![]() 名学生作为样本,采用问卷调查的方法收集数据(参与问卷调查的每名学生只能选择其中一项).并根据调查得到的数据绘制成了如图所示的两幅不完整的统计图.由图中提供的信息,解答下列问题:
名学生作为样本,采用问卷调查的方法收集数据(参与问卷调查的每名学生只能选择其中一项).并根据调查得到的数据绘制成了如图所示的两幅不完整的统计图.由图中提供的信息,解答下列问题:
(1)求n的值;
(2)若该校学生共有1200人,试估计该校喜爱看电视的学生人数;
(3)若调查到喜爱体育活动的4名学生中有3名男生和1名女生,现从这4名学生中任意抽取2名学生,求恰好抽到2名男生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数y1=![]() 的图象与一次函数y2=
的图象与一次函数y2=![]() 的图象交于点A,B,点B的横坐标实数4,点P(1,m)在反比例函数y1=
的图象交于点A,B,点B的横坐标实数4,点P(1,m)在反比例函数y1=![]() 的图象上.
的图象上.
(1)求反比例函数的表达式;
(2)观察图象回答:当x为何范围时,y1>y2;
(3)求△PAB的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com