
 ,△DCQ的面积为y1平方厘米,△PCQ的面积为y2平方厘米.
,△DCQ的面积为y1平方厘米,△PCQ的面积为y2平方厘米.

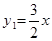 .图象如图所示:
.图象如图所示:
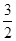 厘米,AC=12厘米;
厘米,AC=12厘米;
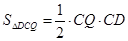 ,CD=3,CQ=x,
,CD=3,CQ=x,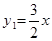 .图象如图所示:
.图象如图所示:
 ,CP=8k-xk,CQ=x,
,CP=8k-xk,CQ=x,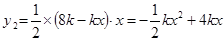 .
.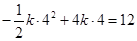 .解得
.解得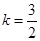
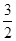 厘米,AC=12厘米;
厘米,AC=12厘米;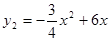 .
.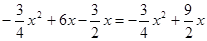 ,
,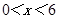 范围,当
范围,当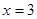 时,
时, 最大.
最大.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:不详 题型:解答题
 的图象经过A(2,0)、B(0,-6)两点。
的图象经过A(2,0)、B(0,-6)两点。
 轴交于点C,连结BA、BC,求△ABC的面积。
轴交于点C,连结BA、BC,求△ABC的面积。查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
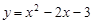 .
.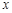 轴下方的部分(不包含与
轴下方的部分(不包含与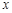 轴的交点)记为G,若直线
轴的交点)记为G,若直线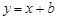 与G 只有一个公共点,则
与G 只有一个公共点,则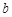 的取值范围是_______.
的取值范围是_______.查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
| 人的年龄x(岁) | x≤60 | 60<x<80 | x≥80 |
| 该人的“老人系数” | 0 | 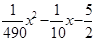 | 1 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 经过
经过 ,
, ,
, 。
。 的坐标,连接
的坐标,连接 ,求证△
,求证△ ∽△
∽△ ;
; 上方的抛物线上是否存在一点M,使S△
上方的抛物线上是否存在一点M,使S△ 最大,求出M的坐标;
最大,求出M的坐标;查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 (
( )与
)与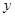 轴交于点
轴交于点 ( 0,4) ,与
( 0,4) ,与 轴交于点
轴交于点 ,
, ,点
,点 的坐标为(4,0).
的坐标为(4,0).
 是线段
是线段 上的动点,过点
上的动点,过点 作
作 ∥
∥ ,交
,交 于点
于点 ,连接
,连接 . 当
. 当 的面积最大时,求点
的面积最大时,求点 的坐标;
的坐标; 轴的动直线与该抛物线交于点
轴的动直线与该抛物线交于点 ,与直线
,与直线 交于点
交于点 ,点
,点 的坐标为(2,0). 问: 是否存在这样的直线,使得
的坐标为(2,0). 问: 是否存在这样的直线,使得 是等腰三角形?若存在,请求出点
是等腰三角形?若存在,请求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com