
 (
( )与
)与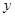 轴交于点
轴交于点 ( 0,4) ,与
( 0,4) ,与 轴交于点
轴交于点 ,
, ,点
,点 的坐标为(4,0).
的坐标为(4,0).
 是线段
是线段 上的动点,过点
上的动点,过点 作
作 ∥
∥ ,交
,交 于点
于点 ,连接
,连接 . 当
. 当 的面积最大时,求点
的面积最大时,求点 的坐标;
的坐标; 轴的动直线与该抛物线交于点
轴的动直线与该抛物线交于点 ,与直线
,与直线 交于点
交于点 ,点
,点 的坐标为(2,0). 问: 是否存在这样的直线,使得
的坐标为(2,0). 问: 是否存在这样的直线,使得 是等腰三角形?若存在,请求出点
是等腰三角形?若存在,请求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由. ;(2)(1,0);(3)(
;(2)(1,0);(3)( ,3)或(
,3)或(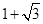 ,3)或(
,3)或(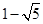 ,2)或(
,2)或(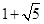 ,2)
,2)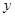 轴交于点
轴交于点 (0,4),与
(0,4),与 轴交于点
轴交于点 (4,0)根据待定系数法即可求得结果;
(4,0)根据待定系数法即可求得结果;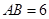 ,
,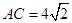 ,
, ,设
,设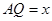 ,
, 的面积用
的面积用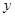 表示,由
表示,由 ∥
∥ 可得
可得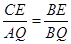 , 即
, 即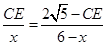 ,即可表示出CE的长,过点
,即可表示出CE的长,过点 作
作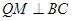 ,垂足为
,垂足为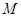 ,在Rt
,在Rt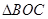 中求得∠B的正弦函数,在Rt
中求得∠B的正弦函数,在Rt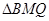 中即可表示出QM的长,从而可以表示出y关于x的函数关系式,再根据二次函数的性质即可求得结果;
中即可表示出QM的长,从而可以表示出y关于x的函数关系式,再根据二次函数的性质即可求得结果;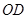 为底边、
为底边、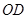 为腰且
为腰且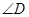 为顶角、
为顶角、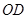 为腰且
为腰且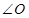 为顶角三种情况分析即可.
为顶角三种情况分析即可. (
( )与
)与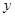 轴交于点
轴交于点 (0,4),与
(0,4),与 轴交于点
轴交于点 (4,0)
(4,0)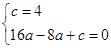 ,解得
,解得 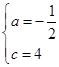
 ;
;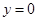 ,则
,则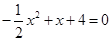 ,解得
,解得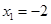 ,
,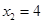
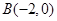
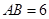 ,
,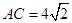 ,
,
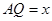 ,
, 的面积用
的面积用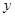 表示,
表示, ∥
∥
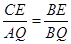 ,即
,即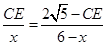
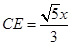
 作
作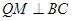 ,垂足为
,垂足为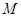
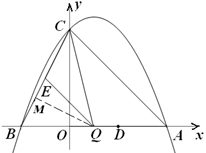
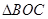 中,
中,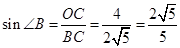
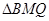 中,
中,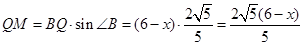

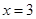 时,
时, 的面积最大是3,即点
的面积最大是3,即点 的坐标为(1,0);
的坐标为(1,0);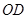 为底边时,点
为底边时,点 的横坐标是1,又点
的横坐标是1,又点 在直线
在直线 上,直线
上,直线 的解析式为
的解析式为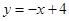 ,所以点
,所以点 的坐标是(1,3),所以点
的坐标是(1,3),所以点 的纵坐标为3,代入
的纵坐标为3,代入 ,得点
,得点 的坐标为(
的坐标为( ,3)或(
,3)或(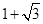 ,3)
,3)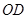 为腰,
为腰,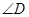 为顶角时,此时点
为顶角时,此时点 是以点
是以点 为圆心,
为圆心,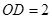 为半径的圆与直线
为半径的圆与直线 的交点,有两个点,点
的交点,有两个点,点 (4,0)与点
(4,0)与点 重合,舍去,点
重合,舍去,点 (2,2),所以点
(2,2),所以点 的纵坐标为2,,代入
的纵坐标为2,,代入 ,得点
,得点 的坐标为(
的坐标为(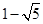 ,2)或(
,2)或(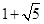 ,2)
,2)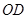 为腰,
为腰,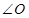 为顶角时,此时点
为顶角时,此时点 应是以点
应是以点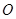 为圆心,
为圆心,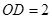 为半径的圆与直线
为半径的圆与直线 的交点,但是点
的交点,但是点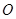 到
到 的距离为
的距离为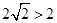 ,所以不存在满足条件的点
,所以不存在满足条件的点 .
.

 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:初中数学 来源:不详 题型:解答题
 ≠0的图像经过点(3,5)、(2,8)、(0,8).
≠0的图像经过点(3,5)、(2,8)、(0,8). ≠0,
≠0, ≠0,且满足
≠0,且满足 ≠0,1,则我们称抛物线
≠0,1,则我们称抛物线 互为“友好抛物线”,请写出当
互为“友好抛物线”,请写出当 时第(1)小题中的抛物线的友好抛物线,并求出这友好抛物线的顶点坐标.
时第(1)小题中的抛物线的友好抛物线,并求出这友好抛物线的顶点坐标.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

 的对称轴为
的对称轴为 )
)查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 ,△DCQ的面积为y1平方厘米,△PCQ的面积为y2平方厘米.
,△DCQ的面积为y1平方厘米,△PCQ的面积为y2平方厘米.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com