
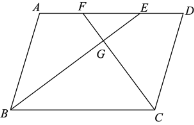
【题目】如图,在□ABCD中,∠ABC,∠BCD的平分线分别交AD于点E,F,BE,CF相交于点G.
(1)求证:BE⊥CF;
(2)若AB=a,CF=b,写出求BE的长的思路.
【答案】(1)见解析;(2)见解析.
【解析】(1)由平行四边形性质得AB∥CD, 可得∠ABC+∠BCD=180°,又BE,CF分别是∠ABC,∠BCD的平分线,所以∠EBC+∠FCB=90°,可得∠BGC=90°;
(2)作EH∥AB交BC于点H,连接AH交BE于点P.证四边形ABHE是菱形,可知AH,BE互相垂直平分,在Rt△ABP中,由勾股定理可求BP,进而可求BE的长.
(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD.
∴∠ABC+∠BCD=180°.
∵BE,CF分别是∠ABC,∠BCD的平分线,
∴∠EBC=![]() ∠ABC,∠FCB=
∠ABC,∠FCB=![]() ∠BCD.
∠BCD.
∴∠EBC+∠FCB=90°.
∴∠BGC=90°.
即BE⊥CF.
(2)求解思路如下:
a.如图,作EH∥AB交BC于点H,连接AH交BE于点P.
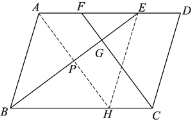
b.由BE平分∠ABC,可证AB=AE,进而可证四边形ABHE是菱形,可知AH,BE互相垂直平分;
c.由BE⊥CF,可证AH∥CF,进而可证四边形AHCF是平行四边形,可求AP=![]() ;
;
d.在Rt△ABP中,由勾股定理可求BP,进而可求BE的长.


 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程x2+(2k+1)x+k2+1=0有两个不等实根x1、x2.
(1)求实数k的取值范围.
(2)若方程两实根x1、x2满足x1+x2=﹣x1x2,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解方程
①(x﹣3)﹣3(3x﹣1)=1
②老师在黑板上出了一道解方程的题![]() =1﹣
=1﹣![]() ,小明马上举手,要求到黑板上做,他是这样做的:
,小明马上举手,要求到黑板上做,他是这样做的:
4(2x﹣1)=1﹣3(x+2)…①
8x﹣4=1﹣3x﹣6…②
8x+3x=1﹣6+4…③
11x=﹣1…④
x=﹣![]() …⑤
…⑤
老师说:小明解一元一次方程的一般步骤都知道却没有掌握好,因此解题时有一步出现了错误,请你指出他错在那一步(填编号),并写出正确的解答过程.
![]() =1﹣
=1﹣![]()
③当m为何值时,关于x的方程5m+3x=1+x的解比关于x的方程2x+m=3m的解小2?
查看答案和解析>>
科目:初中数学 来源: 题型:
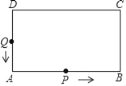
【题目】如图,在长方形ABCD中,AB=14cm,AD=8cm,动点P沿AB边从点A开始,向点B以1cm/s的速度运动;动点Q从点D开始沿DA→AB边,向点B以2cm/s的速度运动.P,Q同时开始运动,当点Q到达B点时,点P和点Q同时停止运动,用t(s)表示运动的时间.
(1)当点Q在DA边上运动时,t为何值,使AQ=AP?
(2)当t为何值时,AQ+AP等于长方形ABCD周长的![]() ?
?
(3)当t为何值时,点Q能追上点P?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们把对角线互相垂直的四边形叫做垂美四边形.
(1)(概念理解)在平行四边形、矩形、菱形、正方形中,一定是垂美四边形的是___________.
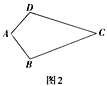
(2)(性质探究)如图2,试探索垂美四边形ABCD的两组对边AB,CD与BC ,AD之间的数量关系,写出证明过程。
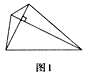
(3)(问题解决)如图3,分别以Rt△ACB的直角边AC和斜边AB为边向外做正方形ACFG和正方形ABDE,连接CE,BG,GE, 已知AC=![]() ,BC=1 求GE的长.
,BC=1 求GE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某届世界杯的小组比赛规则:四个球队进行单循环比赛(每两队赛一场),胜一场得3分,平一场得1分,负一场得0分.某小组比赛结束后,甲、乙、丙、丁四队分别获得第一、二、三、四名,各队的总得分恰好是四个连续奇数,则与乙打平的球队是( )
A. 甲 B. 甲与丁 C. 丙 D. 丙与丁
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将正方体骰子(相对面上的点数分别为1和6、2和5、3和4)放置于水平桌面上,如图1。在图2中,将骰子向右翻滚90°,然后在桌面上按逆时针方向旋转90°,则完成一次变换。若骰子的初始位置为图1所示的状态,那么按上述规则连续完成14次变换后,骰子朝上一面的点数是_____________________。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,三角板ABC的两直角边AC,BC的长分别是40cm和30cm,点G在斜边AB上,且BG=30cm,将这个三角板以G为中心按逆时针旋转90°,至△A′B′C′的位置,那么旋转后两个三角板重叠部分(四边形EFGD)的面积为cm2 . 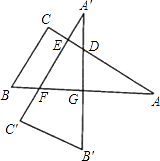
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子里,装有三个分别写有数字﹣1,0,1的乒乓球(形状,大小一样),先从盒子里随即取出一个乒乓球,记下数字后放回盒子,摇匀后再随即取出一个乒乓球,记下数字.
(1)请用树状图或列表的方法求两次取出乒乓球上数字相同的概率;
(2)求两次取出乒乓球上数字之积等于0的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com