
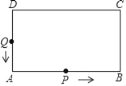
【题目】如图,在长方形ABCD中,AB=14cm,AD=8cm,动点P沿AB边从点A开始,向点B以1cm/s的速度运动;动点Q从点D开始沿DA→AB边,向点B以2cm/s的速度运动.P,Q同时开始运动,当点Q到达B点时,点P和点Q同时停止运动,用t(s)表示运动的时间.
(1)当点Q在DA边上运动时,t为何值,使AQ=AP?
(2)当t为何值时,AQ+AP等于长方形ABCD周长的![]() ?
?
(3)当t为何值时,点Q能追上点P?
【答案】(1)t为![]() 时,AQ=AP.(2)当t为
时,AQ=AP.(2)当t为![]() 或
或![]() 时,AQ+AP等于长方形ABCD周长的
时,AQ+AP等于长方形ABCD周长的![]() .(3)当t为8时,点Q能追上点P.
.(3)当t为8时,点Q能追上点P.
【解析】
(1)找出点Q在DA边上运动且运动时间为ts时,AQ、AP的值,令其相等,即可求出t值;(2)分点Q在DA边上运动时(0≤t≤4)、点Q在AB边上运动时(4≤t≤11)两种情况找出关于t的一元一次方程,解之即可得出结论;(3)点Q追上点P时点Q在AB上运动,令AQ=AP,即可得出关于t的一元一次方程,解之即可得出结论.
(1)当点Q在DA边上运动,运动时间为ts时,AQ=(8﹣2t)cm,AP=tcm,
根据题意得:8﹣2t=t,
解得:t=![]() .
.
答:t为![]() 时,AQ=AP.
时,AQ=AP.
(2)当点Q在DA边上运动时(0≤t≤4),此时AQ=(8﹣2t)cm,AP=t,
根据题意得:8﹣2t+t=2×(14+8)×![]() ,
,
解得:t=![]() ;
;
当点Q在AB边上运动时(4≤t≤11),此时AQ=(2t﹣8)cm,AP=t,
根据题意得:2t﹣8+t=2×(14+8)×![]() ,
,
解得:t=![]() .
.
综上所述:当t为![]() 或
或![]() 时,AQ+AP等于长方形ABCD周长的
时,AQ+AP等于长方形ABCD周长的![]() .
.
(3)根据题意得:2t﹣8=t,
解得:t=8.
答:当t为8时,点Q能追上点P.


科目:初中数学 来源: 题型:
【题目】下列各式中:
①由3x=﹣4系数化为1得x=﹣![]() ;
;
②由5=2﹣x移项得x=5﹣2;
③由![]() 去分母得2(2x﹣1)=1+3(x﹣3);
去分母得2(2x﹣1)=1+3(x﹣3);
④由2(2x﹣1)﹣3(x﹣3)=1去括号得4x﹣2﹣3x﹣9=1.
其中正确的个数有( )
A. 0个 B. 1个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,正方形ABCD的对角线AC,BD相交于点O,E是AC上一点,连接EB,过点A作AM⊥BE,垂足为M,AM与BD相交于F.
(1)直接写出线段OE与OF的数量关系;
(2)如图2,若点E在AC的延长线上,过点A作AM⊥BE ,AM交DB的延长线于点F,其他条件不变.问(1)中的结论还成立吗?如果成立,请给出证明;如果不成立,说明理由;
(3)如图3,当BC=CE时,求∠EAF的度数.
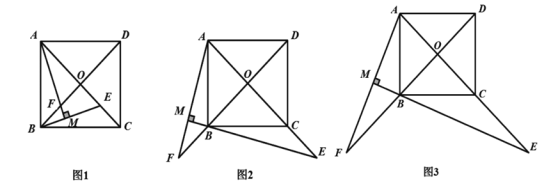
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,射线OA的方向是北偏东15°,射线OB的方向是北偏西40°,∠AOB=∠AOC,射线OD是OB的反向延长线.

(1)射线OC的方向是___________________;
(2)求∠COD的度数;
(3)若射线OE平分∠COD,求∠AOE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从﹣2,﹣1,0,1,2这5个数中,随机抽取一个数记为a,则使关于x的不等式组 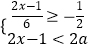 有解,且使关于x的一元一次方程
有解,且使关于x的一元一次方程 ![]() +1=
+1= ![]() 的解为负数的概率为 .
的解为负数的概率为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
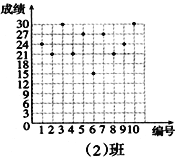
【题目】王老师为了了解学生在数学学习中常见错误的纠正情况,收集整理了学生在作业和考试中的常见错误,编制了10道选择题,每题3分,对他所教的八年(1)班和八年(2)班进行了检测。如图所示表示从两班随机抽取的10名学生的得分情况:
(1)利用图中提供的信息,补全下表:
班级 | 平均分(分) | 中位数(分) | 众数(分) |
八年(1)班 | 24 | 24 | |
八年(2)班 | 24 |
(2)你认为那个班的学生纠错的得分情况比较整齐一些,通过计算说明理由.
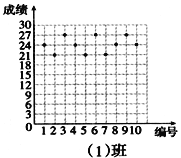
查看答案和解析>>
科目:初中数学 来源: 题型:
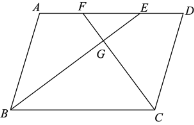
【题目】如图,在□ABCD中,∠ABC,∠BCD的平分线分别交AD于点E,F,BE,CF相交于点G.
(1)求证:BE⊥CF;
(2)若AB=a,CF=b,写出求BE的长的思路.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,∠ABC,∠BCD的平分线分别交AD于点E,F,BE,CF相交于点G.
(1)求证:BE⊥CF;
(2)若AB=a,CF=b,写出求BE的长的思路.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图的数阵是由77个偶数排成:

(1)如图中任意作一个平行四边形框,设左上角的数为x,那么其他3个数从小到大可分别表示为 .
(2)小红说这4个数的和是292,能求出这4个数吗?若存在,请求出这4个数.不存在说明理由.
(3)小明说4个数的和是420,存在这样的数吗?若存在,请求出这4个数,不存在说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com