
如图,已知矩形ABCD中,BC=12, ACB=30º,动点P在线段AC上,从点A向点C以每秒
ACB=30º,动点P在线段AC上,从点A向点C以每秒 个单位的速度运动,设运动时间为t秒,以点P为顶点,作等边△PMN,点M、N在直线BC上,取BC的中点O,以OB为边在Rt△ABC内部作如图所示的矩形BOEF,点E在线段AC上.
个单位的速度运动,设运动时间为t秒,以点P为顶点,作等边△PMN,点M、N在直线BC上,取BC的中点O,以OB为边在Rt△ABC内部作如图所示的矩形BOEF,点E在线段AC上.
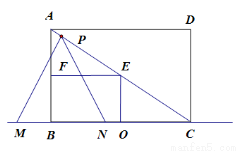


(1)求等边△PMN的边长(用含t的代数式表示);
(2)设等边△PMN和矩形BOEF重合部分面积为S,请直接写出当0≤t≤2时S与t的函数关系式,并写出对应的自变量的取值范围;
(3)点P在运动过程中,是否存在点M,使得△EFM是等腰三角形?若存在,求出对应的t的值;若不存在,请说明理由.
(1) ;(2)
;(2) ;(3)
;(3) ,
, ,
, ,
,
【解析】
试题分析:(1)利用△BPH∽△BAO,得出PH的长,再利用解直角三角形求出PN的长;
(2)根据当0≤t≤1时以及当t=1时和当t=2时,分别求出S的值;
(3)分三种情况①EF=MF,②EF=ME,③MF=ME,分别建立方程求解即可.
试题解析:(1)(1)过P作PH⊥BC于H,

∵BC=12,∠ACB=30°,∴AB= ,∴AC=2AB=
,∴AC=2AB= ,
,
∵AP= ,∴PC=
,∴PC= ,∵△BPH∽△BAO,∴
,∵△BPH∽△BAO,∴ ,∴PH=
,∴PH= ,
,
∵cos30°= ,∴PN=
,∴PN= ,
,
(2)当0≤t≤1时,S1=S四边形EONG,作GH⊥OB于H,如图3,

∵∠GNH=60°,GH= ,∴HN=2,∵PN=NB=8﹣t,∴ON=OB﹣NB,∴ON=12﹣(8﹣t)=4+t,
,∴HN=2,∵PN=NB=8﹣t,∴ON=OB﹣NB,∴ON=12﹣(8﹣t)=4+t,
∴OH=4+t﹣2=2+t,
S1= (2+t+4+t)×
(2+t+4+t)× =
= ,
,
当1<t<2时,如图4,S2=S五边形IFONG,作GH⊥OB于H,

∵AP2= ,∴AF=
,∴AF= ,∴OF=
,∴OF= ,
,
∴EF= ,∴EI=2t﹣2,
,∴EI=2t﹣2,
∴S2=S梯形EONG﹣S△EFI= ,
,
∴ ;
;
(3)由(1)知:MB=4-2t,∴MO=10-2t,∴ ,∴
,∴ ,
,
①当EF=MF时,即 ,∴
,∴ ,∴
,∴ 或
或 <0(舍去),
<0(舍去),
②当EF=ME时,即 ,∴
,∴ ,∴
,∴ 或
或 ,
,
③当MF=ME时,即 ,∴
,∴ .
.
综上所述,当 或
或 或
或 或
或 时,△EFM是等腰三角形.
时,△EFM是等腰三角形.
考点:1.二次函数综合题;2.等边三角形的性质;3.相似三角形的判定与性质.


科目:初中数学 来源:2014-2015学年重庆市九年级上学期期中考试数学试卷(解析版) 题型:选择题
甲、乙、丙、丁四人进行射击测试,每人10次射击的平均成绩恰好是9.4环,方差分别是 =0.90,
=0.90, =1.22,
=1.22, =0.43,
=0.43, =1.68,在本次射击测试中,成绩最稳定的是( )
=1.68,在本次射击测试中,成绩最稳定的是( )
A.甲 B.乙 C.丙 D.丁
查看答案和解析>>
科目:初中数学 来源:2014-2015学年重庆市等五校九年级上学期期中联考数学试卷(解析版) 题型:选择题
已知二次函数 (
( )的图象如图所示,①
)的图象如图所示,① >0,②
>0,② >
> ,③
,③ (m为任意实数),④
(m为任意实数),④ <0,以下结论中正确的个数是( )
<0,以下结论中正确的个数是( )

A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中数学 来源:2014-2015学年重庆市等五校九年级上学期期中联考数学试卷(解析版) 题型:选择题
如图,直线AB∥CD,∠A=70?,∠C=40?,则∠E等于 ( )

A.30° B.40° C.60° D.70°
查看答案和解析>>
科目:初中数学 来源:2014-2015学年重庆市校七年级12月月考数学试卷(解析版) 题型:选择题
在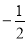 ,—|12|,—20,
,—|12|,—20,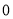 ,
,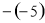 中,负数的个数有( );
中,负数的个数有( );
A.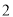 个 B.
个 B.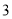 个 C.
个 C.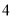 个 D.
个 D.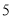 个
个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com