练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    如图，A，B是小河同侧的两个村庄，为解决吃水问题，两村合资在河边修一个水站．
    （1）为使水能同时到达A村和B村，求水站的位置；
    （2）为使到A村和B村的管道总长最短，求水站的位置．
    考点：作图—应用与设计作图
    专题：
    分析：（1）利用线段垂直平分线的性质以及其作法得出即可；
    （2）利用轴对称求最短路径的方法得出即可．
    解答：解：（1）如图1所示：D点即为所求；
    （2）如图2所示：P点即为所求．
    点评：此题主要考查了应用设计与作图，正确把握线段垂直平分线的性质是解题关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    计算：
    （1）4×(-
    1
    2
    -
    3
    4
    +2.5)×3    ；
    （2）（-1）2015×（-12）÷[（-4）2+2×（-5）]．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如果⊙O的半径是4，线段OP的长为3，则点P（　　）
    A、在⊙O上
    B、在⊙O内
    C、在⊙O外
    D、在⊙O上或⊙O内

    查看答案和解析>>

    科目：初中数学 来源： 题型：

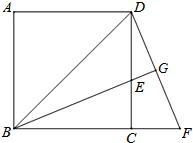    如图，四边形ABCD是正方形，点F在BC延长线上，且BF=BD，G为DF中点，BG与DC交于点E，以下结论正确的有
     
    ．
    ①△BCE≌△DCF        ②E是CD中点
    ③△BCE∽△DGE        ④2DG2=DE•DC．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

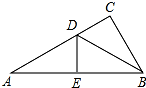    如图，Rt△ABC中，∠C=90°，AB=5，BC=3，D、E分别是AC、AB上的点，且△ADE沿DE折叠后，点A恰好落在点B处，则CD+BD的长为
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，在?ABCD中，AE⊥BD，CF⊥BD，垂足分别为点E，F，点G，H分别为AD，BC的中点，试证明EF和GH互相平分．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    直线AB、CD相交于点O，OE平分∠AOC，∠FOD=90°，∠2：∠3=8：11，求∠1和∠EOF的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

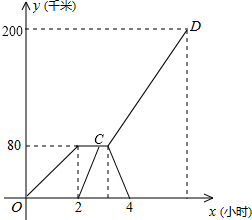    已知A、B两市相距200千米，甲车从A市前往B市运送物资，行驶2小时在M地汽车出现故障不能行驶，立即通知技术人员乘乙车从A市赶去维修（通知时间忽略不计），乙车到达M地后用24分钟修好甲车后以原速度原路返回，同时甲车以原速1.5倍的速度前往B市，如图是两车距A市的路程y（千米）与甲车的行驶时间x（小时）之间的函数图象，结合图象回答下列问题：
    （1）甲车提速后的速度是
     
    千米/小时，点C的坐标是
     
    ，点C的实际意义是
     
    ；
    （2）求乙车返回时y与x之间的函数关系式并写出自变量x的取值范围；
    （3）乙车返回A市多长时间后甲车到达B市．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，等腰直角三角形ABC中，AD是底边BC上的高，现将△ABD沿DC方向平移，使点D和点C重合，若重叠部分（阴影部分）的面积是4，则△ABC的腰长为
     
    ．

    查看答案和解析>>

    同步练习册答案