
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:AD是ABC的边BC上的高,AE是△ABC的外接圆的直径.
已知:AD是ABC的边BC上的高,AE是△ABC的外接圆的直径.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
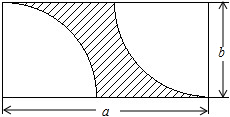 嘉鱼县为创建国家卫生城市,要在人民广场修建一个长方形花坛,面向全县人民征集设计方案,我校同学积极参与.如图所示是七(9)班龚克同学设计的得意之作:
嘉鱼县为创建国家卫生城市,要在人民广场修建一个长方形花坛,面向全县人民征集设计方案,我校同学积极参与.如图所示是七(9)班龚克同学设计的得意之作:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com