
【题目】如图,在△ABC中,AB=AC,点D、E分别是线段BC、AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
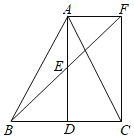
(1)求证:△BDE≌△FAE;
(2)求证:四边形ADCF为矩形.
【答案】(1)见解析;(2)见解析
【解析】
(1)首先根据平行线的性质得到∠AFE=∠DBE,再根据线段中点的定义得到AE=DE,根据全等三角形的判定定理即可得到结论;
(2)根据全等三角形的性质得到AF=BD,推出四边形ADCF是平行四边形,根据等腰三角形的性质得到∠ADC=90°,于是得到结论.
(1)证明:∵AF∥BC,
∴∠AFE=∠DBE,
∵E是线段AD的中点,
∴AE=DE,
∵∠AEF=∠DEB,
∴![]() (AAS);
(AAS);
(2)证明:∵![]() ,
,
∴AF=BD,
∵D是线段BC的中点,
∴BD=CD,
∴AF=CD,
∵AF∥CD,
∴四边形ADCF是平行四边形,
∵AB=AC,
∴![]() ,
,
∴∠ADC=90°,
∴四边形ADCF为矩形.


科目:初中数学 来源: 题型:
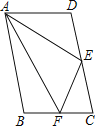
【题目】如图,平行四边形ABCD,点F是BC上的一点,连接AF,∠FAD=60°,AE平分∠FAD,交CD于点E,且点E是CD的中点,连接EF,已知AD=5,CF=3,则EF=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() , 点
, 点![]() 为矩形
为矩形![]() 的边
的边![]() 上一点,连接
上一点,连接![]() ,点
,点![]() 从点
从点![]() 沿折线
沿折线![]() 运动到
运动到![]() 时停止, 点
时停止, 点![]() 从点
从点![]() 沿
沿![]() 运动到点
运动到点![]() 时停止,它们运动
时停止,它们运动![]() 的速度都是
的速度都是![]() ,若点
,若点![]() ,
,![]() 同时开始运动, 设运动时间为
同时开始运动, 设运动时间为![]() ,
,![]() 的面积为
的面积为![]() (当
(当![]() ,
,![]() ,
, ![]() 三点共线时,不妨设
三点共线时,不妨设![]() ).已知
).已知![]() 与
与![]() 之间的函数关系的图象如图
之间的函数关系的图象如图![]() ,则下列结论中错误的是( )
,则下列结论中错误的是( )
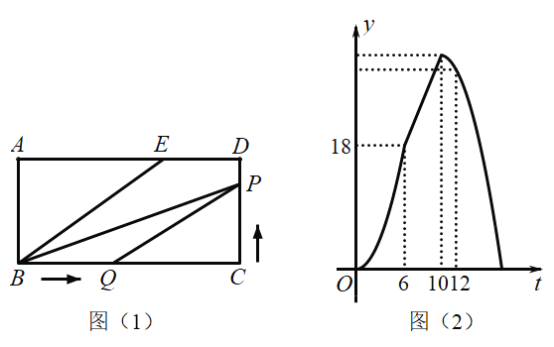
A.![]() B.
B.![]() C.当
C.当![]() 时,
时,![]() D.当
D.当![]() 时,
时,![]() 是等腰三角形
是等腰三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【提出问题】
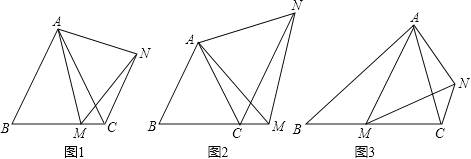
(1)如图1,在等边△ABC中,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等边△AMN,连结CN.求证:∠ABC=∠ACN.
【类比探究】
(2)如图2,在等边△ABC中,点M是BC延长线上的任意一点(不含端点C),其它条件不变,(1)中结论∠ABC=∠ACN还成立吗?请说明理由.
【拓展延伸】
(3)如图3,在等腰△ABC中,BA=BC,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等腰△AMN,使顶角∠AMN=∠ABC.连结CN.试探究∠ABC与∠ACN的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司展销如图所示的长方形工艺品,该工艺品长60cm宽40cm,中间镶有宽度相同的三条丝绸花边.
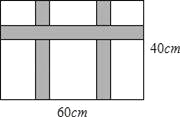
(1)若丝绸花边的面积(阴影面积)为650cm2,求丝绸花边的宽度;
(2)已知该工艺品的成本是40元/件,如果以单价100元/件销售,那么每天可售出200件,另每天还需支付各种费用2000元,根据销售经验,如果将销售单价降低1元,每天可多售出20件,同时,为了完成销售任务,该公司每天至少要销售800件.
(ⅰ)若想每天获利18000元,该公司应该把销售单价定为多少元?
(ⅱ)该公司应该把销售单价定为多少元,才能使每天所获销售利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A的坐标为(0,2),点B的坐标为(1,0),连结AB,以AB为边在第一象限内作正方形ABCD,直线BD交双曲线y═![]() (k≠0)于D、E两点,连结CE,交x轴于点F.
(k≠0)于D、E两点,连结CE,交x轴于点F.

(1)求双曲线y=![]() (k≠0)和直线DE的解析式.
(k≠0)和直线DE的解析式.
(2)求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C在以AB为直径的![]() 上,点D是半圆AB的中点,连接AC,BC,AD,BD,过点D作
上,点D是半圆AB的中点,连接AC,BC,AD,BD,过点D作![]() 交CB的延长线于点H.
交CB的延长线于点H.
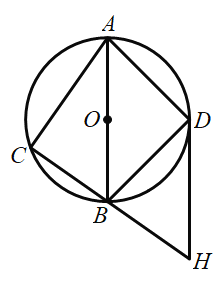
(1)求证:直线DH是![]() 的切线;
的切线;
(2)若![]() ,
,![]() ,求AD,BH的长.
,求AD,BH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某旅游景区为方便游客,修建了一条东西走向的木栈道 AB ,栈道 AB 与景区道路CD 平行.在 C 处测得栈道一端 A 位于北偏西 42°方向,在 D 处测得栈道另一端 B 位于北偏西 32°方向.已知 CD =120 m , BD =80 m ,求木栈道 AB 的长度(结果保留整数) .
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着“节能环保,绿色出行”意识的增强,越来越多的人喜欢骑自行车出行,也给自行车商家带来商机.某自行车行经营的A型自行车去年销售总额为80万元.今年该A型自行车每辆售价预计比去年降低0.02万元.若A型车的销售数量与去年相同,那么今年的销售总额将比去年减少10%,求:
(1)今年经营的A型自行车销售总额是多少万元?
(2)A型自行车去年每辆售价多少万元;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com