
【题目】如图,在平面直角坐标系中,已知点A的坐标为(0,2),点B的坐标为(1,0),连结AB,以AB为边在第一象限内作正方形ABCD,直线BD交双曲线y═![]() (k≠0)于D、E两点,连结CE,交x轴于点F.
(k≠0)于D、E两点,连结CE,交x轴于点F.

(1)求双曲线y=![]() (k≠0)和直线DE的解析式.
(k≠0)和直线DE的解析式.
(2)求![]() 的面积.
的面积.
【答案】(1)y=![]() ,y=3x﹣3;(2)
,y=3x﹣3;(2)![]()
【解析】
(1)作DM⊥y轴于M,通过证得![]() (AAS),求得D的坐标,然后根据待定系数法即可求得双曲线y=
(AAS),求得D的坐标,然后根据待定系数法即可求得双曲线y=![]() (k≠0)和直线DE的解析式.
(k≠0)和直线DE的解析式.
(2)解析式联立求得E的坐标,然后根据勾股定理求得DE和DB,进而求得CN的长,即可根据三角形面积公式求得△DEC的面积.
解:∵点A的坐标为(0,2),点B的坐标为(1,0),
∴OA=2,OB=1,
作DM⊥y轴于M,
∵四边形ABCD是正方形,
∴∠BAD=90°,AB=AD,
∴∠OAB+∠DAM=90°,
∵∠OAB+∠ABO=90°,
∴∠DAM=∠ABO,
在![]() 和
和![]() 中
中
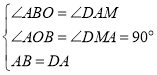 ,
,
∴![]() (AAS),
(AAS),
∴AM=OB=1,DM=OA=2,
∴D(2,3),
∵双曲线![]() 经过D点,
经过D点,
∴k=2×3=6,
∴双曲线为y=![]() ,
,
设直线DE的解析式为y=mx+n,
把B(1,0),D(2,3)代入得![]() ,
,
解得![]() ,
,
∴直线DE的解析式为y=3x﹣3;
(2)连接AC,交BD于N,
∵四边形ABCD是正方形,
∴BD垂直平分AC,AC=BD,
解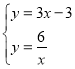
得![]() 或
或![]() ,
,
经检验:两组解都符合题意,
∴E(﹣1,﹣6),
∵B(1,0),D(2,3),
∴DE=![]() =
=![]() ,DB=
,DB=![]() =
=![]() ,
,
∴CN=![]() BD=
BD=![]() ,
,
∴![]()


科目:初中数学 来源: 题型:
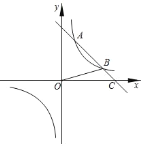
【题目】如图,在平面直角坐标系xOy中,一次函数y=﹣x+4的图象与反比例函数y=![]() (k>0)的图象相交于A,B两点,与x轴相交于点C,连接OB,且
(k>0)的图象相交于A,B两点,与x轴相交于点C,连接OB,且![]() BOC的面积为2.则k=______.
BOC的面积为2.则k=______.
查看答案和解析>>
科目:初中数学 来源: 题型:
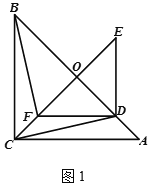
【题目】阅读材料:如图![]() ,
,![]() 与
与![]() 都是等腰直角三角形
都是等腰直角三角形![]() ,且点
,且点![]() 在
在![]() 边上,
边上,![]() ,
,![]() 的中点均为
的中点均为![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,显然,点
,显然,点![]() ,
,![]() ,
,![]() 在同一条直线上,可以证明
在同一条直线上,可以证明![]() ,所以
,所以![]()
解决问题:
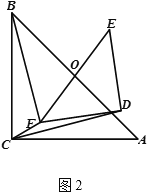
(1) 将图![]() 中的
中的![]() 绕点
绕点![]() 旋转到图
旋转到图![]() 的位置, 猜想此时线段
的位置, 猜想此时线段![]() 与
与![]() 的数量关系,并证明你的结论.
的数量关系,并证明你的结论.
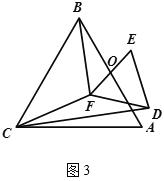
(2) 如图![]() ,若
,若![]() 与
与![]() 都是等边三角形,
都是等边三角形,![]() ,
,![]() 的中点均为
的中点均为![]() ,上述
,上述![]() 中结论仍然成立吗?如果成立,请说明理由;如果不成立,请求出
中结论仍然成立吗?如果成立,请说明理由;如果不成立,请求出![]() 与
与![]() 之间的数量关系.
之间的数量关系.
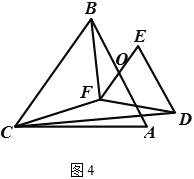
(3) 如图![]() , 若
, 若![]() 与
与![]() 都是等腰三角形,
都是等腰三角形,![]() ,
,![]() 的中点均为
的中点均为![]() ,且顶角
,且顶角![]() ,
,![]() 与
与![]() 之间的数量关系如何(用含
之间的数量关系如何(用含![]() 的式子表示出来)?请直接写出结果.
的式子表示出来)?请直接写出结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
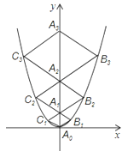
【题目】二次函数y=![]() x2的图象如图,点A0位于坐标原点,点A1,A2,A3…An在y轴的正半轴上,点B1,B2,B3…Bn在二次函数位于第一象限的图象上,点C1,C2,C3…Cn在二次函数位于第二象限的图象上,四边形A0B1A1C1,四边形A1B2A2C2,四边形A2B3A3C3…四边形An﹣1BnAnCn都是菱形,∠A0B1A1=∠A1B2A2=∠A2B3A3…=∠An﹣1BnAn=60°,菱形A2019B2020A2020C2020的周长为________.
x2的图象如图,点A0位于坐标原点,点A1,A2,A3…An在y轴的正半轴上,点B1,B2,B3…Bn在二次函数位于第一象限的图象上,点C1,C2,C3…Cn在二次函数位于第二象限的图象上,四边形A0B1A1C1,四边形A1B2A2C2,四边形A2B3A3C3…四边形An﹣1BnAnCn都是菱形,∠A0B1A1=∠A1B2A2=∠A2B3A3…=∠An﹣1BnAn=60°,菱形A2019B2020A2020C2020的周长为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D、E分别是线段BC、AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
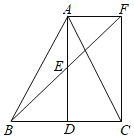
(1)求证:△BDE≌△FAE;
(2)求证:四边形ADCF为矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
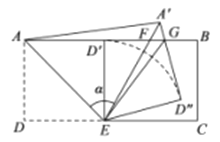
【题目】如图,在矩形ABCD中,![]() ,
,![]() ,把△EAD沿AE折叠,使点D恰好落在AB边上的
,把△EAD沿AE折叠,使点D恰好落在AB边上的![]() 处,再将
处,再将![]() 绕点E顺时针旋转
绕点E顺时针旋转![]() ,得到
,得到![]() ,使得
,使得![]() 恰好经过
恰好经过![]() 的中点F.
的中点F.![]() 交AB于点G,连接
交AB于点G,连接![]() 有如下结论:①
有如下结论:①![]() 的长度是
的长度是![]() ;②弧
;②弧![]() 的长度是
的长度是![]() ;③
;③![]() ;④
;④![]() .上述结论中,所有正确的序号是________.
.上述结论中,所有正确的序号是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在世界环境日(6月5日),学校组织了保护环境知识测试,现从中随机抽取部分学生的成绩作为样本,按“优秀”“良好”“合格”“不合格”四个等级进行统计,绘制了如下尚不完整的统计图表.
测试成绩统计表
等级 | 频数(人数) | 频率 |
优秀 | 30 |
|
良好 |
| 0.45 |
合格 | 24 | 0.20 |
不合格 | 12 | 0.10 |
合计 |
| 1 |

根据统计图表提供的信息,解答下列问题:
(1)表中![]() ________,
________,![]() ________,
________,![]() ________;
________;
(2)补全条形统计图;
(3)若该校有2400名学生参加了本次测试,估计测试成绩等级在良好以上(包括良好)的学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
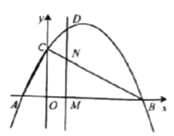
【题目】二次函数![]() 的图象交
的图象交![]() 轴于
轴于![]() 两点,交
两点,交![]() 轴于点
轴于点![]() .动点
.动点![]() 从点
从点![]() 出发,以每秒2个单位长度的速度沿
出发,以每秒2个单位长度的速度沿![]() 方向运动,过点
方向运动,过点![]() 作
作![]() 轴交直线
轴交直线![]() 于点
于点![]() ,交抛物线于点
,交抛物线于点![]() ,连接
,连接![]() .设运动的时间为
.设运动的时间为![]() 秒.
秒.
(1)求二次函数![]() 的表达式:
的表达式:
(2)连接![]() ,当
,当![]() 时,求
时,求![]() 的面积:
的面积:
(3)在直线![]() 上存在一点
上存在一点![]() ,当
,当![]() 是以
是以![]() 为直角的等腰直角三角形时,求此时点
为直角的等腰直角三角形时,求此时点![]() 的坐标;
的坐标;
(4)当![]() 时,在直线
时,在直线![]() 上存在一点
上存在一点![]() ,使得
,使得![]() ,求点
,求点![]() 的坐标
的坐标
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com