
����Ŀ���������x2+px+q��0����������x1��x2����ôx1+x2����p��x1x2��q����������Ͻ��ۣ�����������⣺
(1)��p����4��q��3����x2+px+q��0��������
(2)��֪ʵ��a��b����a2��15a��5��0��b2��15b��5��0����![]() +
+![]() ��ֵ��
��ֵ��
(3)��֪����x�ķ���x2+mx+n��0��(n��0)�����һ��һԪ���η��̣�ʹ�����������ֱ�����֪���������ĵ�����
���𰸡�(1)x1��3��x2��1��(2)-47��2��(3)����x2+![]() x+
x+![]() ��0���������ֱ�����֪���������ĵ���
��0���������ֱ�����֪���������ĵ���
��������
��1������p=-4��q=3���ó�����x2-4x+3=0������⼴�ɣ�
��2������a��b����a2-15a-5=0��b2-15b-5=0���ó�a��b��x2-15x-5=0�Ľ⣬���a+b��ab��ֵ���������![]() +
+![]() ��ֵ��
��ֵ��
��3�����跽��x2+mx+n=0����n��0�����������ֱ���x1��x2���ó�![]() ��
��![]() ���ٸ������һԪ���η��̵��������ֱ�����֪���������ĵ�������������𰸣�
���ٸ������һԪ���η��̵��������ֱ�����֪���������ĵ�������������𰸣�
(1)��p����4��q��3����Ϊx2��4x+3��0��
��ã�x1��3��x2��1
(2)��a��b����a2��15a��5��0��b2��15b��5��0��
��a��b��x2��15x��5��0�Ľ⣬
��a��bʱ��a+b��15��ab����5��
![]() ��
��
��a��bʱ��ԭʽ��2��
(3)�跽��x2+mx+n��0��(n��0)�����������ֱ���x1��x2��
��![]() ��
��![]() ��
��
��x2+![]() x+
x+![]() ��0���������ֱ�����֪���������ĵ���
��0���������ֱ�����֪���������ĵ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У�
�У�![]() ������һ����
������һ����![]() ��
��![]() ��������
��������![]() �����˶�����
�����˶�����![]() �ij���
�ij���![]() ��ʱ��
��ʱ��![]() ֮��Ĺ�ϵ��ͼ���ʾ�����ǣ� ��
֮��Ĺ�ϵ��ͼ���ʾ�����ǣ� ��

A.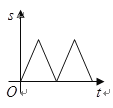 B.
B.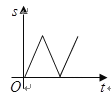
C. D.
D.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��A��B����֮����һ��ɽ������ԭ����A�ص�B�ؾ���C��������A��C��B��ʻ���ֿ�ͨ����������ֱ����ֱ��AB��ʻ����֪AC=10ǧ�ף���B=45�㣬��������ͨ��������A�ص�B�ر�ԭ������ǧ�ף�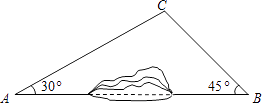
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ABC������ƽ���ڣ��������������ֱ�ΪA��0��3����B��3��4����C��2��2�����������������У�ÿ��С�����εı߳���1����λ���ȣ�
��1��������ABC�Ƶ�A˳ʱ�뷽����ת90���õ�����A1B1C1����д��C1������� ��
��2��������ABC����ԭ��O�����ĶԳƵ���A2B2C2���������ABC����� ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����˫11���ڼ䣬ij���廧���Ա����Ϲ���ijƷ��A��B�������������ۣ�������3��A��4��B��֧��2400Ԫ��������2��A��2��B������֧��1400Ԫ��
��1����A��B�������������ϵ��ۼ۷ֱ��Ƕ���Ԫ��
��2�������廧���Ա����Ϲ���A��B����������10��������ÿ��600Ԫ�������ۣ�����һ��ʱ���ʣ�µ�����ȫ��6�������꣬���ܻ���������3800Ԫ������廧�������۵���������Ƕ��ټ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����10�֣�ij������Ʒר��������7�������9�������������Ϊ355Ԫ������10�������20�������������Ϊ650Ԫ��
��1����ÿ�������ÿ���������������
��2����֪ÿ������Ľ���Ϊ200Ԫ��ÿ������Ľ���Ϊ160Ԫ������ר����ƻ��ò�����17400Ԫ�������������100������Ҫ��������������������������һ�룬����Ϊר������Ʒ���Ҫ��Ľ���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ������ѧϰ����(��ѧ����)�����Խ�����⣺
(a)ijѧϰС����ѧϰʱ�����������⣺��ͼ�٣���Rt��ABC�У���C��90����DΪ��BC��һ�㣬DA��DB��EΪAD�ӳ�����һ�㣬��AEB��120��������BC��EA��EB��������ϵ����֤�����ۣ���Ҿ�̽�����֣�����B��BF��AE��AE���ӳ�����F����ͼ����ʾ������ȫ��������ʹ����������⣬��д�������̣�
(b)�ο�����˼������ķ���������������⣺
��ͼ�ۣ�������ABC�У�AB��AC��HΪAC��һ�㣬��BC���ӳ�����˳��ȡ��E��F����CB���ӳ�����ȡ��BD��ʹEF��DB������E��EG��AC��DH���ӳ����ڵ�G������AF������HDF+��F����BAC��
(1)̽����BAF���CHG��������ϵ��
(2)����ͼ���ҳ�һ�����߶�AF��ȵ��߶Σ���֤����Ľ��ۣ�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com