
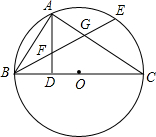
 如图,BC是⊙O的直径,点A在⊙O上,AD⊥BC,垂足为D,$\widehat{AB}$=$\widehat{AE}$,BE分别交AD、AC于点 F、G.
如图,BC是⊙O的直径,点A在⊙O上,AD⊥BC,垂足为D,$\widehat{AB}$=$\widehat{AE}$,BE分别交AD、AC于点 F、G.分析 (1)根据BC是⊙O的直径,AD⊥BC,$\widehat{AB}$=$\widehat{AE}$,推出∠AGB=∠CAD,即可推得FA=FG.
(2)根据BD=DO=2,AD⊥BC,求出∠AOB=60°,再根据$\widehat{AB}$=$\widehat{AE}$,求出∠EOC=60°,即可求出$\widehat{EC}$的长度是多少.
解答 (1)证明:∵BC 是⊙O 的直径,
∴∠BAC=90°,
∴∠ABE+∠AGB=90°;
∵AD⊥BC,
∴∠C+∠CAD=90°;
∵$\widehat{AB}$=$\widehat{AE}$,
∴∠C=∠ABE,
∴∠AGB=∠CAD,
∴FA=FG.
(2)解:如图,连接AO、EO, ,
,
∵BD=DO=2,AD⊥BC,
∴AB=AO,
∵AO=BO,
∴AB=AO=BO,
∴△ABO是等边三角形,
∴∠AOB=60°,
∵$\widehat{AB}$=$\widehat{AE}$,
∴∠AOE=60°,
∴∠EOC=60°,
∴$\widehat{EC}$的弧长=2π×(2×2)×$\frac{60}{360}$=$\frac{4}{3}$π.
点评 此题主要考查了圆周角定理和应用,以及弧长的计算方法,要熟练掌握.


科目:初中数学 来源: 题型:选择题
| A. | ②⑤ | B. | ③⑤ | C. | ②③⑤ | D. | ①②③④⑤ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
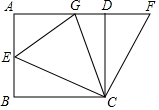 如图1,在边长4的正方形ABCD中,E是AB边上一动点(不与A、B重合),F是AD延长线上一点,且满足DF=BE,以CE为边作∠ECG=45°,交AD于点G.
如图1,在边长4的正方形ABCD中,E是AB边上一动点(不与A、B重合),F是AD延长线上一点,且满足DF=BE,以CE为边作∠ECG=45°,交AD于点G.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在△ABC中,AD为角BAC平分线,DE⊥AB于E,DF⊥AC于F,AB=10厘米,AC=8厘米,△ABC的面积为45平分厘米,求DE的长.
在△ABC中,AD为角BAC平分线,DE⊥AB于E,DF⊥AC于F,AB=10厘米,AC=8厘米,△ABC的面积为45平分厘米,求DE的长.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com