
 如图,某“A”字型监周屋如图①所示,房屋正面的平面图如图②所示,测得∠B=∠C=62°,BC=10.22米,求屋顶A到地面BC的距离(结果精确到0.1米)
如图,某“A”字型监周屋如图①所示,房屋正面的平面图如图②所示,测得∠B=∠C=62°,BC=10.22米,求屋顶A到地面BC的距离(结果精确到0.1米)分析 利用等腰三角形的“三线合一”的性质求得BD=DC=5.11.如图,过点A作AD⊥BC于点D.构建直角△ABD,通过解该直角三角形求得AD的长度.
解答 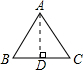 解:如图,过点A作AD⊥BC于点D.
解:如图,过点A作AD⊥BC于点D.
∵∠B=∠C=62°,
∴AB=AC.
∴BD=DC=$\frac{1}{2}$BC=$\frac{1}{2}$×10.22=5.11.
在Rt△ABD中,∠ADB=90°,∠BAC=62°,
tanB=$\frac{AD}{BD}$,
∴AD=BD•tanB=5.11×1.88=9.6068≈9.6(米).
答:屋顶A到地面BC的距离约为9.6米.
点评 本题考查了解直角三角形的应用.主要是正切概念及运算,关键把实际问题转化为数学问题加以计算.


科目:初中数学 来源: 题型:填空题
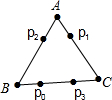 小明观看了阿尔法狗下围棋后,设计了一款电子跳蚤游戏,如图所示的正△ABC边长为12cm,如果电子跳蚤开始在BC边的点P0处,且BP0=4cm.此时第一步从P0跳到AC边的P1(第1次落点)处,且CP1=CP0;第二步从P1跳到AB边的P2(第2次落点)处,且AP2=AP1;第三步P2从跳到BC边的P3(第3次落点)处,且BP3=BP2;…:电子跳蚤按照上述规则已知跳下去,第n次落点为Pn(n为正整数),则点P2015与点P2016之间的距离是4cm.
小明观看了阿尔法狗下围棋后,设计了一款电子跳蚤游戏,如图所示的正△ABC边长为12cm,如果电子跳蚤开始在BC边的点P0处,且BP0=4cm.此时第一步从P0跳到AC边的P1(第1次落点)处,且CP1=CP0;第二步从P1跳到AB边的P2(第2次落点)处,且AP2=AP1;第三步P2从跳到BC边的P3(第3次落点)处,且BP3=BP2;…:电子跳蚤按照上述规则已知跳下去,第n次落点为Pn(n为正整数),则点P2015与点P2016之间的距离是4cm.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 等边三角形是中心对称图形 | |
| B. | 三点可以确定一个圆 | |
| C. | 矩形的四个顶点一定共圆 | |
| D. | 三角形三条角平分线的交点为三角形的外心 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
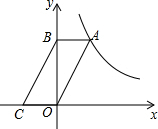 如图,在平面直角坐标系中,点A在函数y=$\frac{k}{x}(k>0,x>0)$的图象上,过点A作AB∥x轴交y轴于点B,连结OA,过点B作BC∥OA交x轴于点C,若△BOC的面积是2,则k=4.
如图,在平面直角坐标系中,点A在函数y=$\frac{k}{x}(k>0,x>0)$的图象上,过点A作AB∥x轴交y轴于点B,连结OA,过点B作BC∥OA交x轴于点C,若△BOC的面积是2,则k=4.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com