
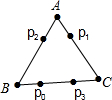
 小明观看了阿尔法狗下围棋后,设计了一款电子跳蚤游戏,如图所示的正△ABC边长为12cm,如果电子跳蚤开始在BC边的点P0处,且BP0=4cm.此时第一步从P0跳到AC边的P1(第1次落点)处,且CP1=CP0;第二步从P1跳到AB边的P2(第2次落点)处,且AP2=AP1;第三步P2从跳到BC边的P3(第3次落点)处,且BP3=BP2;…:电子跳蚤按照上述规则已知跳下去,第n次落点为Pn(n为正整数),则点P2015与点P2016之间的距离是4cm.
小明观看了阿尔法狗下围棋后,设计了一款电子跳蚤游戏,如图所示的正△ABC边长为12cm,如果电子跳蚤开始在BC边的点P0处,且BP0=4cm.此时第一步从P0跳到AC边的P1(第1次落点)处,且CP1=CP0;第二步从P1跳到AB边的P2(第2次落点)处,且AP2=AP1;第三步P2从跳到BC边的P3(第3次落点)处,且BP3=BP2;…:电子跳蚤按照上述规则已知跳下去,第n次落点为Pn(n为正整数),则点P2015与点P2016之间的距离是4cm. 分析 首先根据题意,分别计算电子跳骚的位置和三角形的顶点的距离,找到循环的规律:经过6次跳,电子跳蚤回到起跳点.根据这一规律确定第2015次、第2016次落点的位置,再根据△BP0P5是等边三角形,即P2015P2016=P5P0,从而确定P2015与P2016之间的距离.
解答 解:因为BP0=4,根据题意,CP0=12-4=8,
第一步从P0到P1,CP1=CP0=8;AP1=12-8=4,
第二步从P1到P2,AP2=AP1=4;BP2=12-4=8,
第三步从P2到P3,BP3=BP2=8;CP3=12-8=4,
第四步从P3到P4,CP4=CP3=4;AP4=12-4=8,
第五步从P4到P5,AP5=AP4=8;BP5=12-8=4,
第六步从P5到P6,BP6=BP5=4;
由此可知,P6点与P0点重合,
又因为2015÷6=335…5,2016÷6=336,
所以P2015点与P5点重合,则点P2015与B点之间的距离为BP5=4,
P2016点与P0点重合,则点P2016与B点之间的距离为BP0=4,
又∵∠B=60°,
故△BP0P5是等边三角形,即P2015P2016=P5P0=4cm,
故答案为:4cm.
点评 本题考查了规律型:图形的变化和等边三角形的判定和性质,此题主要是能够根据题意正确计算出有关线段的长,发现电子跳蚤的落点的循环规律,从而完成计算.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
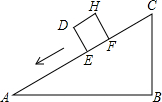 一个正方体物体沿斜坡向下滑动,其截面如图所示.正方形DEFH的边长为2米,坡角∠A=30°,∠B=90°,BC=6米.当正方形DEFH运动到什么位置,即当AE为多少米时?有DC2=AE2+BC2.
一个正方体物体沿斜坡向下滑动,其截面如图所示.正方形DEFH的边长为2米,坡角∠A=30°,∠B=90°,BC=6米.当正方形DEFH运动到什么位置,即当AE为多少米时?有DC2=AE2+BC2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,?ABCD中,对角线AC、BD交于点O,点E是BC的中点.若OE=4cm,则AB的长为( )
如图,?ABCD中,对角线AC、BD交于点O,点E是BC的中点.若OE=4cm,则AB的长为( )| A. | 4cm | B. | 8cm | C. | 2cm | D. | 6cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
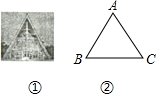 如图,某“A”字型监周屋如图①所示,房屋正面的平面图如图②所示,测得∠B=∠C=62°,BC=10.22米,求屋顶A到地面BC的距离(结果精确到0.1米)
如图,某“A”字型监周屋如图①所示,房屋正面的平面图如图②所示,测得∠B=∠C=62°,BC=10.22米,求屋顶A到地面BC的距离(结果精确到0.1米)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com