
分析 分两种情况,如图1,连接OB根据垂径定理得到OB=10,BD=$\frac{1}{2}$BC=8,由勾股定理得到OD=$\sqrt{O{B}^{2}-B{D}^{2}}$=6,于是得到△ABC的面积=$\frac{1}{2}$BC•AD=$\frac{1}{2}$×16×16=128cm2,如图2,AD=10-6=4,于是得到△ABC的面积=$\frac{1}{2}$BC•AD=$\frac{1}{2}$×4×16=32cm2.
解答 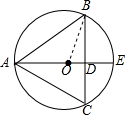 解:如图1,连接OB,∵AE=20cm,弦BC=16cm,且BC⊥AE于D,
解:如图1,连接OB,∵AE=20cm,弦BC=16cm,且BC⊥AE于D,
∴OB=10,BD=$\frac{1}{2}$BC=8,
∴OD=$\sqrt{O{B}^{2}-B{D}^{2}}$=6,
∴AD=10+6=16,
∴△ABC的面积=$\frac{1}{2}$BC•AD=$\frac{1}{2}$×16×16=128cm2,
如图2,AD=10-6=4,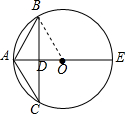
∴△ABC的面积=$\frac{1}{2}$BC•AD=$\frac{1}{2}$×4×16=32cm2,
综上所述:△ABC的面积是128cm2或32cm2.
故答案为:128cm2或32cm2.
点评 本题考查了垂径定理,勾股定理,三角形的面积的计算,熟练掌握垂径定理是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m=4,n=32 | B. | m=4,n=-32 | C. | m=-4,n=32 | D. | m=-4,n=-32 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x(x-1)=45 | B. | x(x+1)=45 | C. | x(x+1)=90 | D. | x(x-1)=90 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ∠A+∠B=∠C | B. | ∠A=∠B=∠C/2 | C. | ∠A=90°-∠B | D. | ∠A-∠B=90° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
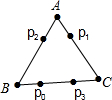 小明观看了阿尔法狗下围棋后,设计了一款电子跳蚤游戏,如图所示的正△ABC边长为12cm,如果电子跳蚤开始在BC边的点P0处,且BP0=4cm.此时第一步从P0跳到AC边的P1(第1次落点)处,且CP1=CP0;第二步从P1跳到AB边的P2(第2次落点)处,且AP2=AP1;第三步P2从跳到BC边的P3(第3次落点)处,且BP3=BP2;…:电子跳蚤按照上述规则已知跳下去,第n次落点为Pn(n为正整数),则点P2015与点P2016之间的距离是4cm.
小明观看了阿尔法狗下围棋后,设计了一款电子跳蚤游戏,如图所示的正△ABC边长为12cm,如果电子跳蚤开始在BC边的点P0处,且BP0=4cm.此时第一步从P0跳到AC边的P1(第1次落点)处,且CP1=CP0;第二步从P1跳到AB边的P2(第2次落点)处,且AP2=AP1;第三步P2从跳到BC边的P3(第3次落点)处,且BP3=BP2;…:电子跳蚤按照上述规则已知跳下去,第n次落点为Pn(n为正整数),则点P2015与点P2016之间的距离是4cm.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 等边三角形是中心对称图形 | |
| B. | 三点可以确定一个圆 | |
| C. | 矩形的四个顶点一定共圆 | |
| D. | 三角形三条角平分线的交点为三角形的外心 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com