
【题目】在同一直角坐标系中,抛物线C1:y=ax2﹣2x﹣3与抛物线C2:y=x2+mx+n关于y轴对称,C2与x轴交于A、B两点,其中点A在点B的左侧.
(1)求抛物线C1,C2的函数表达式;
(2)求A、B两点的坐标;
(3)在抛物线C1上是否存在一点P,在抛物线C2上是否存在一点Q,使得以AB为边,且以A、B、P、Q四点为顶点的四边形是平行四边形?若存在,求出P、Q两点的坐标;若不存在,请说明理由.

【答案】(1)C1的函数表示式为y=x2﹣2x﹣3,C2的函数表达式为y=x2+2x﹣3;(2)A(﹣3,0),B(1,0);(3)存在满足条件的点P、Q,其坐标为P(﹣2,5),Q(2,5)或P(2,﹣3),Q(﹣2,﹣3).
【解析】
(1)由对称可求得a、n的值,则可求得两函数的对称轴,可求得m的值,则可求得两抛物线的函数表达式;
(2)由C2的函数表达式可求得A、B的坐标;
(3)由题意可知AB只能为平行四边形的边,利用平行四边形的性质,可设出P点坐标,表示出Q点坐标,代入C2的函数表达式可求得P、Q的坐标.
解:(1)∵C1、C2关于y轴对称,
∴C1与C2的交点一定在y轴上,且C1与C2的形状、大小均相同,
∴a=1,n=﹣3,
∴C1的对称轴为x=1,
∴C2的对称轴为x=﹣1,
∴m=2,
∴C1的函数表示式为y=x2﹣2x﹣3,C2的函数表达式为y=x2+2x﹣3;
(2)在C2的函数表达式为y=x2+2x﹣3中,令y=0可得x2+2x﹣3=0,解得x=﹣3或x=1,
∴A(﹣3,0),B(1,0);
(3)存在.
∵AB只能为平行四边形的一边,
∴PQ∥AB且PQ=AB,
由(2)可知AB=1﹣(﹣3)=4,
∴PQ=4,
设P(t,t2﹣2t﹣3),则Q(t+4,t2﹣2t﹣3)或(t﹣4,t2﹣2t﹣3),
①当Q(t+4,t2﹣2t﹣3)时,则t2﹣2t﹣3=(t+4)2+2(t+4)﹣3,解得t=﹣2,
∴t2﹣2t﹣3=4+4﹣3=5,
∴P(﹣2,5),Q(2,5);
②当Q(t﹣4,t2﹣2t﹣3)时,则t2﹣2t﹣3=(t﹣4)2+2(t﹣4)﹣3,解得t=2,
∴t2﹣2t﹣3=4﹣4﹣3=﹣3,
∴P(2,﹣3),Q(﹣2,﹣3),
综上可知存在满足条件的点P、Q,其坐标为P(﹣2,5),Q(2,5)或P(2,﹣3),Q(﹣2,﹣3).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
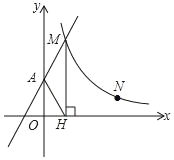
【题目】如图,直线y=2x+2与y轴交于A点,与反比例函数y=![]() (x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=2.
(x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=2.
(1)求H点的坐标及k的值;
(2)点P在y轴上,使△AMP是以AM为腰的等腰三角形,请直接写出所有满足条件的P点坐标;
(3)点N(a,1)是反比例函数y=![]() (x>0)图象上的点,点Q(m,0)是x轴上的动点,当△MNQ的面积为3时,请求出所有满足条件的m的值.
(x>0)图象上的点,点Q(m,0)是x轴上的动点,当△MNQ的面积为3时,请求出所有满足条件的m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的是一个地球仪及它的平面图,在平面图中,点A、B分别为地球仪的南、北极点,直线AB与放置地球仪的平面交于点D,所夹的角度约为67°,半径OC所在的直线与放置它的平面垂直,垂足为点E,DE=15cm,AD=14cm.

(1)求半径OA的长(结果精确到0.1cm,参考数据:sin67°≈0.92,cos67°≈0.39,tan67°≈2.36)
(2)求扇形BOC的面积(π取3.14,结果精确到1cm)
查看答案和解析>>
科目:初中数学 来源: 题型:
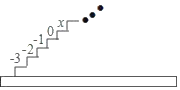
【题目】如图,阶梯图的每个台阶上都标着一个数,从下到上的第1个至第4个台阶上依次标着﹣3,﹣2,﹣1,0,且任意相邻四个台阶上数的和都相等.
(1)求第五个台阶上的数x是多少?
(2)求前21个台阶上的数的和是多少?
(3)发现:数的排列有一定的规律,第n个﹣2出现在第 个台阶上;
(4)拓展:如果倩倩小同学一步只能上1个或者2个台阶,那么她上第一个台阶的方法有1种:1=1,上第二个台阶的方法有2种:1+1=2或2=2,上第三个台阶的方祛有3种:1+1+1=3、1+2=3或2+1=3,…,她上第五个台阶的方法可以有 种.
查看答案和解析>>
科目:初中数学 来源: 题型:
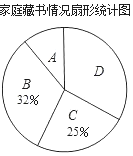
【题目】在“书香校园”活动中,某校为了解学生家庭藏书情况,随机抽取本校部分学生进行调查,并绘制成部分统计图表如下:
类别 | 家庭藏书m本 | 学生人数 |
A | 0≤m≤25 | 20 |
B | 26≤m≤100 | a |
C | 101≤m≤200 | 50 |
D | m≥201 | 66 |
根据以上信息,解答下列问题:
(1)该调查的样本容量为_____,a=_____;
(2)在扇形统计图中,“A”对应扇形的圆心角为_____°;
(3)若该校有2000名学生,请估计全校学生中家庭藏书200本以上的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
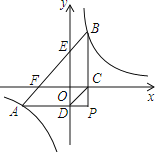
【题目】如图,![]() 的直角顶点P在第四象限,顶点A、B分别落在反比例函数
的直角顶点P在第四象限,顶点A、B分别落在反比例函数![]() 图象的两支上,且
图象的两支上,且![]() 轴于点C,
轴于点C,![]() 轴于点D,AB分别与x轴,y轴相交于点F和
轴于点D,AB分别与x轴,y轴相交于点F和![]() 已知点B的坐标为
已知点B的坐标为![]() .
.
![]() 填空:
填空:![]() ______;
______;
![]() 证明:
证明:![]() ;
;
![]() 当四边形ABCD的面积和
当四边形ABCD的面积和![]() 的面积相等时,求点P的坐标.
的面积相等时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果批发商经销一种高档水果,如果每千克盈利5元,每天可售出200千克,经市场调查发现,在进价不变的情况下,若每千克涨价0.1元,销售量将减少1千克
(1)现该商场保证每天盈利1500元,同时又要照顾顾客,那么每千克应涨价多少元?
(2)若该商场单纯从经济利益角度考虑,这种水果每千克涨价多少元,使该商场获利最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
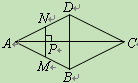
【题目】如图,点P是菱形ABCD的对角线AC上的一个动点,过点P垂直于AC的直
线交菱形ABCD的边于M、N两点.设AC=2,BD=1,AP=x,△AMN的面积为y,则
y关于x的函数图象大致形状是【 】

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点P从△ABC的顶点B出发,沿B→C→A匀速运动到点A,图2是点P运动时,线段BP的长度y随时间x变化的函数关系图象,其中M为曲线部分的最低点下列说法错误的是( )
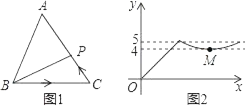
A. △ABC是等腰三角形B. AC边上的高为4
C. △ABC的周长为16D. △ABC的面积为10
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com