
【题目】如图,点P是菱形ABCD的对角线AC上的一个动点,过点P垂直于AC的直
线交菱形ABCD的边于M、N两点.设AC=2,BD=1,AP=x,△AMN的面积为y,则
y关于x的函数图象大致形状是【 】
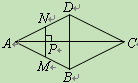

【答案】C
【解析】△AMN的面积= ![]() AP×MN,通过题干已知条件,用x分别表示出AP、MN,根据所得的函数,利用其图象,可分两种情况解答:(1)0<x≤1;(2)1<x<2;
AP×MN,通过题干已知条件,用x分别表示出AP、MN,根据所得的函数,利用其图象,可分两种情况解答:(1)0<x≤1;(2)1<x<2;
解:(1)当0<x≤1时,如图,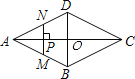
在菱形ABCD中,AC=2,BD=1,AO=1,且AC⊥BD;
∵MN⊥AC,
∴MN∥BD;
∴△AMN∽△ABD,
∴![]() =
=![]() ,
,
即,![]() =
=![]() ,MN=x;
,MN=x;
∴y=![]() AP×MN=
AP×MN=![]() x2(0<x≤1),
x2(0<x≤1),
∵![]() >0,
>0,
∴函数图象开口向上;
(2)当1<x<2,如图,
同理证得,△CDB∽△CNM,![]() =
=![]() ,
,
即![]() =
=![]() ,MN=2-x;
,MN=2-x;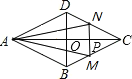
∴y=![]()
AP×MN=![]() x×(2-x),
x×(2-x),
y=-![]() x2+x;
x2+x;
∵-![]() <0,
<0,
∴函数图象开口向下;
综上答案C的图象大致符合.
故选:C.
本题考查了二次函数的图象,考查了学生从图象中读取信息的数形结合能力,体现了分类讨论的思想.


科目:初中数学 来源: 题型:
【题目】如图,四边形![]() 是矩形纸片,
是矩形纸片,![]() .对折矩形纸片
.对折矩形纸片![]() ,使
,使![]() 与
与![]() 重合,折痕为
重合,折痕为![]() ;展平后再过点
;展平后再过点![]() 折叠矩形纸片,使点
折叠矩形纸片,使点![]() 落在
落在![]() 上的点
上的点![]() ,折痕
,折痕![]() 与
与![]() 相交于点
相交于点![]() ;再次展平,连接
;再次展平,连接![]() ,
,![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() .以下结论:①
.以下结论:①![]() ;②
;②![]() ;③
;③![]() ;④△
;④△![]() 是等边三角形; ⑤
是等边三角形; ⑤![]() 为线段
为线段![]() 上一动点,
上一动点,![]() 是
是![]() 的中点,则
的中点,则![]() 的最小值是
的最小值是![]() .其中正确结论的序号是( ).
.其中正确结论的序号是( ).
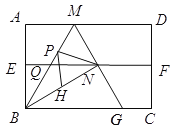
A. ①②④B. ①④⑤C. ①③④D. ①②③⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在同一直角坐标系中,抛物线C1:y=ax2﹣2x﹣3与抛物线C2:y=x2+mx+n关于y轴对称,C2与x轴交于A、B两点,其中点A在点B的左侧.
(1)求抛物线C1,C2的函数表达式;
(2)求A、B两点的坐标;
(3)在抛物线C1上是否存在一点P,在抛物线C2上是否存在一点Q,使得以AB为边,且以A、B、P、Q四点为顶点的四边形是平行四边形?若存在,求出P、Q两点的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
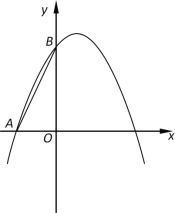
【题目】如图,抛物线![]() 经过点A(﹣2,0),点B(0,4).
经过点A(﹣2,0),点B(0,4).
(1)求这条抛物线的表达式;
(2)P是抛物线对称轴上的点,联结AB、PB,如果∠PBO=∠BAO,求点P的坐标;
(3)将抛物线沿y轴向下平移m个单位,所得新抛物线与y轴交于点D,过点D作DE∥x轴交新抛物线于点E,射线EO交新抛物线于点F,如果EO=2OF,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
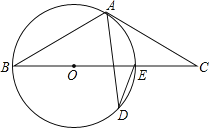
【题目】如图,BE是O的直径,点A和点D是⊙O上的两点,过点A作⊙O的切线交BE延长线于点.
(1)若∠ADE=25°,求∠C的度数;
(2)若AB=AC,CE=2,求⊙O半径的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为改善生态环境,防止水土流失,某村计划在江汉堤坡种植白杨树,现甲、乙两家林场有相同的白杨树苗可供选择,其具体销售方案如下:
甲林场 | 乙林场 | ||
购树苗数量 | 销售单价 | 购树苗数量 | 销售单价 |
不超过1000棵时 | 4元/棵 | 不超过2000棵时 | 4元/棵 |
超过1000棵的部分 | 3.8元/棵 | 超过2000棵的部分 | 3.6元/棵 |
设购买白杨树苗x棵,到两家林场购买所需费用分别为y甲(元)、y乙(元).
(1)该村需要购买1500棵白杨树苗,若都在甲林场购买所需费用为 元,若都在乙林场购买所需费用为 元;
(2)分别求出y甲、y乙与x之间的函数关系式;
(3)如果你是该村的负责人,应该选择到哪家林场购买树苗合算,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
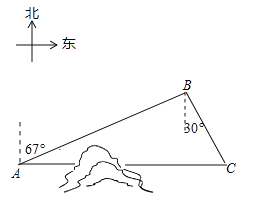
【题目】如图,C地在A地的正东方向,因有大山阻隔,由A地到C地需绕行B地,已知B地位于A地北偏东67°方向,距离A地520km,C地位于B地南偏东30°方向,若打通穿山隧道,建成两地直达高铁,求A地到C地之间高铁线路的长.(结果保留整数)
(参考数据:sin67°≈![]() ,cos67°≈
,cos67°≈![]() ,tan67°≈
,tan67°≈![]() ,
,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过点P作PA,PB,分别与以OA为半径的半圆切于A,B,延长AO交切线PB于点C,交半圆与于点D.
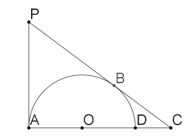
(1)若PC=5,AC=4,求BC的长;
(2)设DC:AD=1:2,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
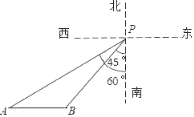
【题目】在某海域,一艘海监船在P处检测到南偏西45°方向的B处有一艘不明船只,正沿正西方向航行,海监船立即沿南偏西60°方向以40海里/小时的速度去截获不明船只,经过1.5小时,刚好在A处截获不明船只,求不明船只的航行速度.(![]() ≈1.41,
≈1.41,![]() ≈1.73,结果保留一位小数).
≈1.73,结果保留一位小数).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com