
����Ŀ����ͼ������ͼ��ÿ��̨���϶�����һ���������µ��ϵĵ�1������4��̨�������α��ũ�3����2����1��0�������������ĸ�̨�������ĺͶ���ȣ�
��1��������̨���ϵ���x�Ƕ��٣�
��2����ǰ21��̨���ϵ����ĺ��Ƕ��٣�
��3�����֣�����������һ���Ĺ��ɣ���n����2�����ڵ��� ����̨���ϣ�
��4����չ�����ٻٻСͬѧһ��ֻ����1������2��̨�ף���ô���ϵ�һ��̨�ķ�����1�֣�1��1���ϵڶ���̨�ķ�����2�֣�1+1��2��2��2���ϵ�����̨�ķ�����3�֣�1+1+1��3��1+2��3��2+1��3���������ϵ����̨�ķ����������� ���֣�
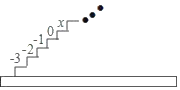
���𰸡���1�������̨���ϵ���x�ǩ�3��2��-33��3����4n��2����4��8
��������
��1������������4��������ӿɵã����ݡ������ĸ�̨�������ĺͶ���ȡ��г��������ɵ�x��
��2�����ݡ�̨���ϵ�������ÿ4��һѭ�������ɵã�
��3��̨���ϵ�������ÿ4��һѭ�������ݹ��ɿɵý��ۣ�
��4�����ݵ�һ����1��̨��2��̨��������ۿɵý��ۣ�
��1����������3��2��1+0����2��1+0+x��
x����3��
�𣺵����̨���ϵ���x�ǩ�3��
��2��������֪��̨���ϵ�������ÿ4��һѭ����
��3��2��1+0����6��
��21��4��5��1��
��5������6��+����3������33��
��ǰ21��̨���ϵ����ĺ��ǩ�33��
��3����һ����2�ڵ�2��̨���ϣ�
�ڶ�����2�ڵ�6��̨���ϣ�
��������2�����ڵ�10��̨���ϣ�
��
��n����2�����ڵڣ�4n��2����̨���ϣ�
�ʴ�Ϊ��4n��2����
��4���ϵ����̨�ķ�����1+1+1+1+1��5��1�֣�
1+1+1+2��5��1+2+2��5��1+2+1+1��5��1+1+2+1��5��4�֣�
2+2+1��5��2+1+2��5��2+1+1+1��5��3�֣�
��1+4+3��8�֣�
�����ϵ����̨�ķ���������8�֣�
�ʴ�Ϊ8��


 ����С״Ԫ��������������ϵ�д�
����С״Ԫ��������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���з��̽�Ӧ���⣺
ij�̳���8��Ԫ����һ���¿�������ϼܺ�ܿ�����һ�գ��̳��ֽ��������ڶ������ֳ����������ǵ�һ�ε�2��������������4Ԫ/�����������ȥ17.6��Ԫ��
��1�����̳���һ�������������ټ���
��2���̳��������ֳ���ʱ��ÿ�����۶���58Ԫ��ʣ��150��ʱ�����۳��ۣ�ȫ�����꣮�����������������̳���ӯ������Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���![]() �Ǿ���ֽƬ��
�Ǿ���ֽƬ��![]() �����۾���ֽƬ
�����۾���ֽƬ![]() ��ʹ
��ʹ![]() ��
��![]() �غϣ��ۺ�Ϊ
�غϣ��ۺ�Ϊ![]() ��չƽ���ٹ���
��չƽ���ٹ���![]() �۵�����ֽƬ��ʹ��
�۵�����ֽƬ��ʹ��![]() ����
����![]() �ϵĵ�
�ϵĵ�![]() ���ۺ�
���ۺ�![]() ��
��![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ���ٴ�չƽ������
���ٴ�չƽ������![]() ��
��![]() ���ӳ�
���ӳ�![]() ��
��![]() �ڵ�
�ڵ�![]() �����½��ۣ���
�����½��ۣ���![]() ����
����![]() ����
����![]() ������
������![]() �ǵȱ������Σ� ��
�ǵȱ������Σ� ��![]() Ϊ�߶�
Ϊ�߶�![]() ��һ���㣬
��һ���㣬![]() ��
��![]() ���е㣬��
���е㣬��![]() ����Сֵ��
����Сֵ��![]() ��������ȷ���۵������( ).
��������ȷ���۵������( ).
A. �٢ڢ�B. �٢ܢ�C. �٢ۢ�D. �٢ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
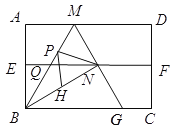
����Ŀ�����ǹ涨���Զ��κ���y=ax2+bx+c�Ķ�����ϵ��a��2��Ϊһ����ϵ����һ����ϵ��bΪ��������һ�κ���y=2ax+b�������κ���y=ax2+bx+c�����Ӻ������������������κ���y=ax2+bx+c����һ�κ���y=2ax+b����ĸ��������
��1����һ�κ���y=2x-4�Ƕ��κ���y=ax2+bx+c�����Ӻ��������Ҷ��κ��������㣨3��0������˶��κ����Ľ���ʽ���������꣮
��2�������Ӻ�����y=x-6����ĸ����������СֵΪ1������ĸ�������ĺ�������ʽ��
��3����֪���κ���y=-x2-4x+8�����Ӻ�����ͼ��ֱ��l��x�ᡢy�ύ��C��D���㣬����PΪ���κ���y=-x2-4x+8�Գ����Ҳ��ϵĶ��㣬����PCD����������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ƕ��壺��һ��Խ���ȵ��ı��ν������ȶԽ��ı�������
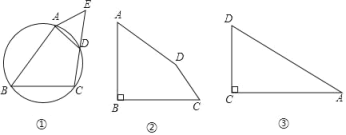
��1����ͼ�����ı���ABCD�ڽ�����O����E��CD���ӳ����ϣ���AE��AD��֤�����ı���ABCE�����ȶԽ��ı�������
��2����ͼ���������ȶԽ��ı�����ABCD�У���DAB����BCD��53������B��90����sin53���![]() ��cos53���
��cos53���![]() ��tan53���
��tan53���![]() .
.
��3����ͼ������Rt��ACD�У���ACD��90������DAC��30����CD��4�����ı���ABCD�����ȶԽ��ı�����������B����D����BD�����ֵ���� ����ֱ��д�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�OABC�Ķ���A��x���ϣ�����B������Ϊ��6��4������ֱ��l�����㣨1��0�����ҽ�OABC�ָ�������ȵ������֣���ֱ��l�ĺ�������ʽ�ǣ�������
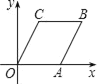
A. y��x+1B. ![]() C. y��3x��3D. y��x��1
C. y��3x��3D. y��x��1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͬһֱ������ϵ�У�������C1��y��ax2��2x��3��������C2��y��x2+mx+n����y��Գƣ�C2��x�ύ��A��B���㣬���е�A�ڵ�B����࣮
��1����������C1��C2�ĺ�������ʽ��
��2����A��B��������ꣻ
��3����������C1���Ƿ����һ��P����������C2���Ƿ����һ��Q��ʹ����ABΪ�ߣ�����A��B��P��Q�ĵ�Ϊ������ı�����ƽ���ı��Σ������ڣ����P��Q��������ꣻ�������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
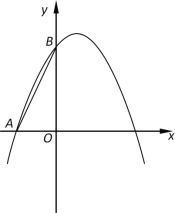
����Ŀ����ͼ��������![]() ������A����2��0������B��0��4��.
������A����2��0������B��0��4��.
��1�������������ߵı���ʽ��
��2��P�������߶Գ����ϵĵ㣬����AB��PB�������PBO=��BAO�����P�����ꣻ
��3������������y������ƽ��m����λ����������������y�ύ�ڵ�D������D��DE��x�ύ���������ڵ�E������EO�����������ڵ�F�����EO=2OF����m��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������P��PA��PB���ֱ�����OAΪ�뾶�İ�Բ����A��B���ӳ�AO������PB�ڵ�C������Բ���ڵ�D��
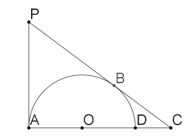
��1����PC=5��AC=4����BC�ij���
��2����DC:AD=1:2����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com