练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
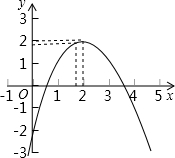
    12．已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，有下列结论：①abc＞0；②9a+4b+c＜0；③9a-c+1＞0；④a＜-$\frac{1}{8}$，其中，正确的结论的个数是（　　）
    A．1B．2C．3D．4

    分析 根据图象信息，确定顶点，设出顶点式，根据图象经过（0，-2），求出a、b、c，判断选项即可．

    解答 解：从图象可以看出，顶点坐标为（2，2），且经过（0，-2），
    设解析式为：y=a（x-2）2+2，
    把（0，-2）代入解析式得，a=-1，
    则解析式为：y=-x2+4x-2，
    ∴a=-1，b=4，c=-2，
    abc＞0，①正确；
    9a+4b+c=5＞0，②错误；
    9a-c+1=-6＜0，③错误；
    a=-1＜-$\frac{1}{8}$，④正确．
    故选：B．

    点评 本题考查的是二次函数的图象与系数的关系，熟练运用待定系数法求二次函数的解析式是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

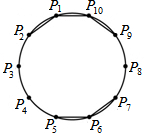    2．如图是P1、P2、…、P10十个点在圆上的位置图，且此十点将圆周分成十等分．今小玉连接P1P2、P1P10、P9P10、P5P6、P6P7，判断小玉再连接下列哪一条线段后，所形成的图形不是轴对称图形？（　　）
    A．P2P3B．P4P5C．P7P8D．P8P9

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

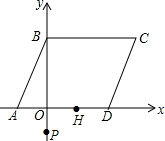    3．如图，?ABCD中，A（-2，0）、B（0，4），AD在x轴上，且OD=2OA．
    （1）求顶点C、D的坐标及CD的长；
    （2）求直线AC的解析式；
    （3）x轴下方的y轴上是否存在点P，使得直线CP把?ABCD的面积分成1：6两部分？若存在，求出P的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．解不等式：3（2-y）＜2（y-2）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．某商店一种商品的定价为每件20元，商店为了促销，决定如果购买5件以上，则超过5件的部分打七折．用表达式表示购买这种商品的货款y（元）与购买数量x（件）之间的函数关系．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．若m是不等式组$\left\{\begin{array}{l}{2（1-x）＜x+8}\\{\frac{3x-2}{6}＜\frac{x-1}{3}}\end{array}\right.$的最大整数解，求1+m+m2+…+m2014．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．为了探究代数式$\sqrt{{x^2}+4}+\sqrt{{{（{9-x}）}^2}+1}$的最小值，小明巧妙的运用了“数形结合”思想．具体方法是这样的：如图，C为线段BD上一动点，分别过点B、D作AB⊥BD，ED⊥BD，连接AC、EC．已知AB=2，DE=1，BD=9，设BC=x．则$AC=\sqrt{{x^2}+4}$，$CE=\sqrt{{{（{9-x}）}^2}+1}$，则问题即转化成求AC+CE的最小值．
    （1）我们知道当A、C、E在同一直线上时，AC+CE的值最小，于是可求得$\sqrt{{x^2}+4}+\sqrt{{{（{9-x}）}^2}+1}$的最小值等于，3$\sqrt{10}$，此时x=6；
    （2）请你根据上述的方法和结论，试构图求出代数式$\sqrt{{x}^{2}+25}$+$\sqrt{{x}^{2}-24x+153}$的最小值及对应的x的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

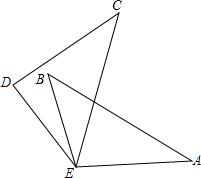    1．如图，已知△EAB≌△DCE，AB、EC分别是两个三角形的最长边，∠A=∠C=35°，∠CDE=100°，∠DEB=10°，求∠AEC的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    6．如图①，在矩形纸片ABCD中，AB=$\sqrt{3}$+1，AD=$\sqrt{3}$．
    （1）如图②，将矩形纸片向上方翻折，使点D恰好落在AB边上的D′处，压平折痕交CD于点E，则折痕AE的长为$\sqrt{6}$．
    （2）如图③，再将四边形BCED′沿D′E向左翻折，压平后得四边形B′C′ED′，B′C′交AE于点F，则四边形B′FED′的面积为$\sqrt{3}$-$\frac{1}{2}$．
    （3）如图④，将图②中的△AED′绕点E顺时针旋转α角，得△A′ED″，使得EA′恰好经过顶点B，求弧D′D″的长$\frac{5\sqrt{3}π}{12}$．（结果保留π）

    查看答案和解析>>

    同步练习册答案