
【题目】已知△ABC,AB=AC,∠BAC=∠EPF=90°,点P是BC的中点,两边PE、PF分别交AB,AC于E、F,连接EF、AP.有下列结论①AE=CF ②EF=AP ③△EPF是等腰直角三角形④![]() ,其中正确的有( )个
,其中正确的有( )个

A. 1 B. 2 C. 3 D. 4
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】大学生小张利用暑假50天在一超市勤工俭学,被安排销售一款成本为40元/件的新型商品,此类新型商品在第x天的销售量p件与销售的天数x的关系如下表:
x(天) | 1 | 2 | 3 | … | 50 |
p(件) | 118 | 116 | 114 | … | 20 |
销售单价q(元/件)与x满足:当1≤x<25时q=x+60;当25≤x≤50时q=40+ ![]() .
.
(1)请分析表格中销售量p与x的关系,求出销售量p与x的函数关系.
(2)求该超市销售该新商品第x天获得的利润y元关于x的函数关系式.
(3)这50天中,该超市第几天获得利润最大?最大利润为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】操作探究:已知在纸面上有一数轴(如图所示).
![]()
操作一:
(1)折叠纸面,使1表示的点与-1表示的点重合,则-3表示的点与________表示的点重合;
操作二:
(2)折叠纸面,使-1表示的点与3表示的点重合,回答以下问题:
①5表示的点与数________表示的点重合;
②若数轴上A、B两点之间距离为11(A在B的左侧),且A、B两点经折叠后重合,求A、B两点表示的数是多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某研究性学习小组,为了解本校七年级学生一天中做家庭作业所用的大致时间(时间以整数记,单位:分),对本校的七年级学生做了抽样调查,并把调查得到的所有数据(时间)进行整理,分成五个时间段,绘制成统计图如图所示,请结合统计图中提供的信息,回答下列问题.
(1)这个研究性学习小组所抽取的学生有多少人?
(2)在被调查的学生中,一天做家庭作业所用的大致时间超过120分(不包括120分)的人数占被调查学生总人数的百分之几?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公交公司有A、B型两种客车,它们的载客量和租金如下表:
A | B | |
载客量(人/辆) | 45 | 30 |
租金 (元/辆) | 400 | 280 |
红星中学根据实际情况,计划租用A、B型客车共5辆,同时送八年级师生到基地参加社会实践活动.设租用A型客车x辆,根据要求回答下列问题.
(1)若要保证租车费用不超过1900元,求x的最大值;
(2)在(1)的条件下,若八年级师生共有195人,请设计一种最省钱的租车方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如下表:
X | ﹣1 | 0 | 1 | 3 |
y | ﹣1 | 3 | 5 | 3 |
下列结论:
(1)ac<0;
(2)当x>1时,y的值随x值的增大而减小.
(3)3是方程ax2+(b﹣1)x+c=0的一个根;
(4)当﹣1<x<3时,ax2+(b﹣1)x+c>0.
其中正确的个数为( )
A.4个
B.3个
C.2个
D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC与△A1B1C1 , 关于点E成中心对称.
(1)画出对称中心E,并写出点E的坐标是 ;
(2)P(a,b)是边上的一点,△ABC经过平移后点P的对应点为P2(a+6,b+2),请画出上述平移后的△A2B2C2 . 并写出点A2坐标为 ,点B2坐标为 ;
(3)直接判断并写出△A1B1C1 , 与△A2B2C2的位置关系为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
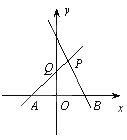
【题目】如图,直线PA是一次函数y=x+1的图象,直线PB是一次函数y=-2x+2的图象.
(1)求A、B、P三点的坐标;
(2)求四边形PQOB的面积;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在Rt△ABC中,∠ACB=90°,O是AB上一点,以OA为半径的⊙O切BC于点D,交AC于点E,且AD=BD.
(1)求证:DE∥AB;
(2)如图2,连接OC,求cos∠ACO的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com