
如图,直线 与抛物线
与抛物线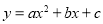 的图象都经过
的图象都经过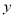 轴上的D点,抛物线与
轴上的D点,抛物线与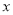 轴交于A、B两点,其对称轴为直线
轴交于A、B两点,其对称轴为直线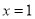 ,且
,且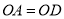 .直线
.直线 与
与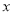 轴交于点C(点C在点B的右侧).则下列命题中正确命题的个数是( ).
轴交于点C(点C在点B的右侧).则下列命题中正确命题的个数是( ).
① ; ②
; ② ; ③
; ③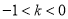 ; ④
; ④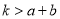 ; ⑤
; ⑤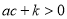
A.1 B.2 C.3 D.4

C.
【解析】
试题分析:∵抛物线开口向上,
∴a>0.
∵抛物线对称轴是x=1,
∴b<0且b=-2a.
∵抛物线与y轴交于正半轴,
∴c>0.
∴①abc>0错误;
②3a+b>0正确;
∵直线y=kx+c经过一、二、四象限,
∴k<0.
∵OA=OD,
∴点A的坐标为(c,0).
直线y=kx+c当x=c时,y>0,
∴kc+c>0可得k>-1.
∴③-1<k<0正确;
∵直线y=kx+c与抛物线y=ax2+bx+c的图象有两个交点
∴ax2+bx+c=kx+c,
得x1=0,x2= .
.
由图象知x2>1,
∴ >1
>1
∴k>a+b
∴④k>a+b正确;
∵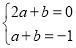 ,
,
∴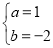 .
.
又∵c<1,
∴ac<1.
∵-1<k<0,
∴-1<ac+k<1.
∴⑤ac+k>0错误.
正确的命题有3个。
故选C.
考点:二次函数图象与系数的关系.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:2013-2014学年重庆市万州区岩口复兴学校九年级下学期期中命题四数学试卷(解析版) 题型:选择题
已知:如图,l1∥l2,∠1=50°, 则∠2的度数是 ( )
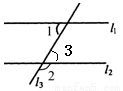
A.120° B.50° C.40° D.130°
查看答案和解析>>
科目:初中数学 来源:2013-2014学年重庆市万州区岩口复兴学校九年级下学期期中命题三数学试卷(解析版) 题型:填空题
如果关于x的不等式组: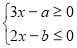 ,的整数解仅有1,2,那么适合这个不等式组的整数a,b组成的有序数对[a,b]共有 个。
,的整数解仅有1,2,那么适合这个不等式组的整数a,b组成的有序数对[a,b]共有 个。
查看答案和解析>>
科目:初中数学 来源:2013-2014学年重庆市九年级3月月考数学试卷(解析版) 题型:解答题
如图,菱形ABCD中,点E,M在A,D上,且CD=CM,点F为AB上的点,且∠ECF=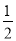 ∠B
∠B
(1)若菱形ABCD的周长为8,且∠D=67.5°,求△MCD的面积。
(2)求证:BF=EF-EM
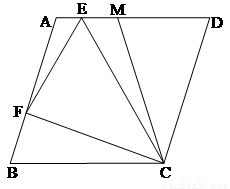
查看答案和解析>>
科目:初中数学 来源:2013-2014学年重庆市九年级3月月考数学试卷(解析版) 题型:填空题
已知平面直角坐标系内A、B两点的坐标分别为A(0,0)和B(2,2),现有四张正面分别标有数字-2,0,2,4的不透明卡片,它们除了数字不同外其余全部相同.先将它们背面朝上,洗匀后从中任取一张,将该卡片上的数记为x,将卡片放回后从中再取一张,将该卡片上的数字记为y,记P点的坐标为P(x,y),则以P、A、B三点所构成的三角形为等腰直角三角形的概率为______
查看答案和解析>>
科目:初中数学 来源:2013-2014学年重庆市九年级3月月考数学试卷(解析版) 题型:选择题
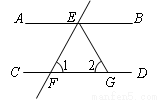
如图,已知AB∥CD,直线EF分别交AB、CD于点E、F,EG平分∠BEF,若∠1=70°,则∠2的度数是( )
A.70° B.55° C.60° D.50°
查看答案和解析>>
科目:初中数学 来源:2013-2014学年重庆市九年级下学期期中考试数学试卷(解析版) 题型:解答题
如图①,在□ABCD中,对角线AC⊥AB,BC=10,tan∠B=2.点E是BC边上的动点,过点E作EF⊥BC于点E,交折线AB-AD于点F,以EF为边在其右侧作正方形EFGH,使EH边落在射线BC上.点E从点B出发,以每秒1个单位的速度在BC边上运动,当点E与点C重合时,点E停止运动,设点E的运动时间为t( )秒.
)秒.
(1)□ABCD的面积为 ;当t= 秒时,点F与点A重合;
(2)点E在运动过程中,连接正方形EFGH的对角线EG,得△EHG,设△EHG与△ABC的重叠部分面积为S,请直接写出S与t的函数关系式以及对应的自变量t的取值范围;
(3)作点B关于点A的对称点Bˊ,连接CBˊ交AD边于点M(如图②),当点F在AD边上时,EF与对角线AC交于点N,连接MN得△MNC.是否存在时间t,使△MNC为等腰三角形?若存在,请求出使△MNC为等腰三角形的时间t;若不存在,请说明理由.
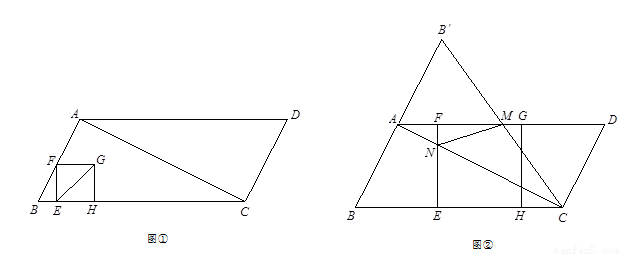
查看答案和解析>>
科目:初中数学 来源:2013-2014学年重庆市九年级下学期期中考试数学试卷(解析版) 题型:选择题
用棋子按下列方式摆图形,第一个图形有1枚棋子,第二个图形有5枚棋子,第三个图形有12枚棋子,…依此规律,第7个图形比第6个图形多( )枚棋子
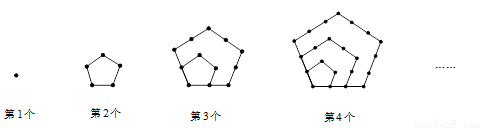
A.20 B.19 C.18 D.17
查看答案和解析>>
科目:初中数学 来源:2013-2014学年辽宁省丹东市九年级第一次模拟考试数学试卷(解析版) 题型:解答题
在△ABC和△DEF中,∠C=∠F=90°.有如下五张背面完全相同的纸牌①、②、③、④、⑤,其正面分别写有五个不同的等式,小民将这五张纸牌背面朝上洗匀后先随机摸出一张(不放回),再随机摸出一张.请结合以上条件,解答下列问题.
(1)、你认为 和 组合,△ABC和△DEF不一定全等,
(2)用树状图(或列表法)表示两次摸牌所有可能出现的结果(纸牌用①、②、③、④、⑤表示);
(3)用两次摸牌的结果和∠C=∠F=90°作为条件,求能满足△ABC和△DEF全等的概率.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com