
【题目】如图,在Rt△ABC中,∠ACB=90°,D、E分别是AB、AC的中点,连接CD,过E作EF∥DC交BC的延长线于F.
(1)证明:四边形CDEF是平行四边形;
(2)若四边形CDEF的周长是25cm,AC的长为5cm,求线段AB的长度.

【答案】(1)证明见解析;(2)AB=13cm,
【解析】(1)由三角形中位线定理推知ED∥FC,2DE=BC,然后结合已知条件“EF∥DC”,利用两组对边相互平行得到四边形DCFE为平行四边形;
(2)根据在直角三角形中,斜边上的中线等于斜边的一半得到AB=2DC,即可得出四边形DCFE的周长=AB+BC,故BC=25﹣AB,然后根据勾股定理即可求得;
(1)∵D、E分别是AB、AC的中点,F是BC延长线上的一点,
∴ED是Rt△ABC的中位线,
∴ED∥FC.BC=2DE,
又 EF∥DC,
∴四边形CDEF是平行四边形;
(2)∵四边形CDEF是平行四边形;
∴DC=EF,
∵DC是Rt△ABC斜边AB上的中线,
∴AB=2DC,
∴四边形DCFE的周长=AB+BC,
∵四边形DCFE的周长为25cm,AC的长5cm,
∴BC=25﹣AB,
∵在Rt△ABC中,∠ACB=90°,
∴AB2=BC2+AC2,即AB2=(25﹣AB)2+52,
解得,AB=13cm.


科目:初中数学 来源: 题型:
【题目】提出问题:
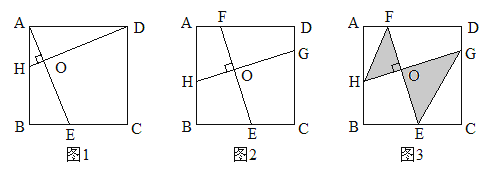
(1)如图1,在正方形ABCD中,点E,H分别在BC,AB上,若AE⊥DH于点O,求证:AE=DH;
类比探究:
(2)如图2,在正方形ABCD中,点H,E,G,F分别在边AB,BC,CD,DA上,若EF⊥HG于点O,探究线段EF与HG的数量关系,并说明理由;
综合运用:
(3)在(2)问条件下,HF∥GE,如图3所示,已知BE=EC=2,EO=2FO,求图中阴影部分的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,小明有5张写着不同数字的卡片,请你按要求抽出卡片,完成下列各题:
(1)若从中抽出2张卡片,且这2个数字的差最小,应如何抽取?最小值是多少?
(2)若从中抽出2张卡片,且这2个数字的积最大,应如何抽取?最小值是多少?
(3)若从中抽出4张卡片,运用加、减、乘、除、乘方、括号等运算符号,使得结果为24.请写出运算式.(只需写出一种)
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AH⊥BC,BF平分∠ABC,BE⊥BF,EF∥BC,以下四个结论①AH⊥EF,②∠ABF=∠EFB,③AC∥BE,④∠E=∠ABE.正确的是( )

A. ①②③④ B. ①② C. ①③④ D. ①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
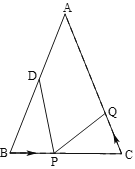
【题目】如图,已知△ABC中,AB=AC=10cm,BC=8cm,∠B=∠C,点D为AB的中点.
(1)如果点P在线段BC上以3cm/s的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.
①若点Q的运动速度与点P的运动速度相等,经过1s后,△BPD与△CQP是否全等,请说明理由;
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为时________cm/s,在运动过程中能够使△BPD与△CQP全等.(直接填答案)
(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿△ABC三边运动,求经过多长时间点P与点Q第一次在△ABC的哪条边上相遇?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市十一优惠顾客,若一次性购物不超过300元不优惠,超过300元时按全额9折优惠.一位顾客第一次购物付款120元,第二次购物付款288元,若这两次购物合并成一次性付款可节省_____元.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com