
【题目】已知直线l1:y=x+3与x轴交于点A,与y轴交于点B,且与双曲线y= ![]() 交于点C(1,a).
交于点C(1,a).
(1)试确定双曲线的函数表达式;
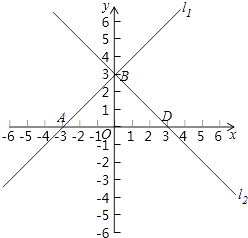
(2)将l1沿y轴翻折后,得到l2 , 画出l2的图象,并求出l2的函数表达式;
(3)在(2)的条件下,点P是线段AC上点(不包括端点),过点P作x轴的平行线,分别交l2于点M,交双曲线于点N,求S△AMN的取值范围.
【答案】
(1)
解:令x=1代入y=x+3,
∴y=1+3=4,
∴C(1,4),
把C(1,4)代入y= ![]() 中,
中,
∴k=4,
∴双曲线的解析式为:y= ![]()
(2)
解:如图所示,
设直线l2与x轴交于点D,
由题意知:A与D关于y轴对称,
∴D的坐标为(3,0),
设直线l2的解析式为:y=ax+b,
把D与B的坐标代入上式,
得: ![]() ,
,
∴解得: ![]() ,
,
∴直线l2的解析式为:y=﹣x+3
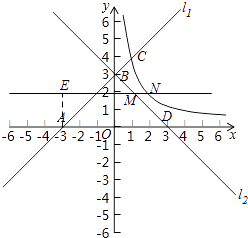
(3)
解:设M(3﹣t,t),
∵点P在线段AC上移动(不包括端点),
∴0<t<4,
∴PN∥x轴,
∴N的纵坐标为t,
把y=t代入y= ![]() ,
,
∴x= ![]() ,
,
∴N的坐标为( ![]() ,t),
,t),
∴MN= ![]() ﹣(3﹣t)=
﹣(3﹣t)= ![]() +t﹣3,
+t﹣3,
过点A作AE⊥PN于点E,
∴AE=t,
∴S△AMN= ![]() AEMN,
AEMN,
= ![]() t(
t( ![]() +t﹣3)
+t﹣3)
= ![]() t2﹣
t2﹣ ![]() t+2
t+2
= ![]() (t﹣
(t﹣ ![]() )2+
)2+ ![]() ,
,
由二次函数性质可知,当0≤t≤ ![]() 时,S△AMN随t的增大而减小,当
时,S△AMN随t的增大而减小,当 ![]() <t≤4时,S△AMN随t的增大而增大,
<t≤4时,S△AMN随t的增大而增大,
∴当t= ![]() 时,S△AMN可取得最小值为
时,S△AMN可取得最小值为 ![]() ,
,
当t=4时,S△AMN可取得最大值为4,
∵0<t<4
∴ ![]() ≤S△AMN<4
≤S△AMN<4
【解析】本题考查函数的综合问题,涉及待定系数法求一次函数解析式和反比例函数解析式,三角形面积等知识,由于有动点,所以难度较高,需要学生利用参数去表示相关坐标,然后求出函数关系式.(1)令x=1代入一次函数y=x+3后求出C的坐标,然后把C代入反比例函数解析式中即可求出k的值;(2)设直线l2与x轴交于D,由题意知,A与D关于y轴对称,所以可以求出D的坐标,再把B点坐标代入y=ax+b即可求出直线l2的解析式;(3)设M的纵坐标为t,由题意可得M的坐标为(3﹣t,t),N的坐标为( ![]() ,t),进而得MN=
,t),进而得MN= ![]() +t﹣3,又可知在△ABM中,MN边上的高为t,所以可以求出S△AMN与t的关系式.
+t﹣3,又可知在△ABM中,MN边上的高为t,所以可以求出S△AMN与t的关系式.
【考点精析】通过灵活运用确定一次函数的表达式和三角形的面积,掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法;三角形的面积=1/2×底×高即可以解答此题.


科目:初中数学 来源: 题型:
【题目】已知某道判断题的五个选项中有两个正确答案,该题满分为4分,得分规则是:选出两个正确答案且没有选错误答案得4分;只选出一个正确答案且没有选错误答案得2分;不选或所选答案中有错误答案得0分.
(1)任选一个答案,得到2分的概率是;
(2)请利用树状图或表格求任选两个答案,得到4分的概率;
(3)如果小明只能确认其中一个答案是正确的,此时的最佳答题策略是
A.只选确认的那一个正确答案
B.除了选择确认的那一个正确答案,再任选一个
C.干脆空着都不选了.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据卫生防疫部门要求,游泳池必须定期换水,清洗.某游泳池周五早上8:00打开排水孔开始排水,排水孔的排水速度保持不变,期间因清洗游泳池需要暂停排水,游泳池的水在11:30全部排完.游泳池内的水量Q(m2)和开始排水后的时间t(h)之间的函数图象如图所示,根据图象解答下列问题: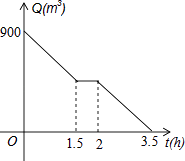
(1)暂停排水需要多少时间?排水孔排水速度是多少?
(2)当2≤t≤3.5时,求Q关于t的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是线段AB上的点,点C,D分别是线段OA,OB的中点,小明很轻松地求得CD=![]() AB.他在反思过程中突发奇想:若点O在线段AB的延长线上或在直线AB外,则原有的结论“CD=
AB.他在反思过程中突发奇想:若点O在线段AB的延长线上或在直线AB外,则原有的结论“CD=![]() AB”仍然成立吗?请帮小明解决此问题(当点O在线段AB的延长线上时,请画图分析该结论是否成立,并说明理由;当点O在直线AB外时,作出图形,通过度量说明该结论是否成立).
AB”仍然成立吗?请帮小明解决此问题(当点O在线段AB的延长线上时,请画图分析该结论是否成立,并说明理由;当点O在直线AB外时,作出图形,通过度量说明该结论是否成立).
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为3cm,P,Q分别从B,A出发沿BC,AD方向运动,P点的运动速度是1cm/秒,Q点的运动速度是2cm/秒,连接A,P并过Q作QE⊥AP垂足为E.
(1)求证:△ABP∽△QEA;
(2)当运动时间t为何值时,△ABP≌△QEA;
(3)设△QEA的面积为y,用运动时刻t表示△QEA的面积y(不要求考t的取值范围).(提示:解答(2)(3)时可不分先后)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王老师家买了一套新房,其结构如图所示(单位:m).他打算将卧室铺上木地板,其余部分铺上地砖.
(1)木地板和地砖分别需要多少平方米?
(2)如果地砖的价格为每平方米x元,木地板的价格为每平方米3x元,那么王老师需要花多少钱?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y= ![]() x+2与双曲线相交于点A(m,3),与x轴交于点C.
x+2与双曲线相交于点A(m,3),与x轴交于点C. 
(1)求双曲线解析式;
(2)点P在x轴上,如果△ACP的面积为3,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com