
【题目】如图,点O是线段AB上的点,点C,D分别是线段OA,OB的中点,小明很轻松地求得CD=![]() AB.他在反思过程中突发奇想:若点O在线段AB的延长线上或在直线AB外,则原有的结论“CD=
AB.他在反思过程中突发奇想:若点O在线段AB的延长线上或在直线AB外,则原有的结论“CD=![]() AB”仍然成立吗?请帮小明解决此问题(当点O在线段AB的延长线上时,请画图分析该结论是否成立,并说明理由;当点O在直线AB外时,作出图形,通过度量说明该结论是否成立).
AB”仍然成立吗?请帮小明解决此问题(当点O在线段AB的延长线上时,请画图分析该结论是否成立,并说明理由;当点O在直线AB外时,作出图形,通过度量说明该结论是否成立).
![]()
科目:初中数学 来源: 题型:
【题目】一个不透明的袋中装有红、黄、白三种颜色的球共100个,它们除颜色外都相同,其中黄球的个数是白球个数的2倍少5个,已知从袋中摸出一个红球的概率是 ![]() .
.
(1)求袋中红球的个数;
(2)求从袋中摸出一个球是白球的概率;
(3)取走5个黄球5个白球,求从剩余的球中摸出一个球是红球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】回答下面的例题:
解方程:x2﹣|x|﹣2=0.
解:①x≥0时,原方程化为x2﹣x﹣2=0,解得x1=2,x2=﹣1(不合题意,舍去).
②x<0时,原方程化为x2+x﹣2=0,解得x1=﹣2,x2=1(不合题意,舍去).
∴原方程的根是x1=2,x2=﹣2.
请参照例题解方程x2+|x﹣4|﹣8=0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点O为坐标原点,点B的坐标为(4,3),点A、C在坐标轴上,点P在BC边上,直线l1:y=2x+3,直线l2:y=2x﹣3.
(1)分别求直线l1与x轴,直线l2与AB的交点坐标;
(2)已知点M在第一象限,且是直线l2上的点,若△APM是等腰直角三角形,求点M的坐标;
(3)我们把直线l1和直线l2上的点所组成的图形为图形F.已知矩形ANPQ的顶点N在图形F上,Q是坐标平面内的点,且N点的横坐标为x,请直接写出x的取值范围(不用说明理由).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次中学生田径运动会上,根据参加男子跳高初赛的运动员的成绩(单位:m),绘制出如下的统计图①和图②,请根据相关信息,解答下列问题:
(1)图1中a的值为;
(2)求统计的这组初赛成绩数据的平均数、众数和中位数;
(3)根据这组初赛成绩,由高到低确定9人进入复赛,请直接写出初赛成绩为1.65m的运动员能否进入复赛.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AD=6,AE⊥BD,垂足为E,ED=3BE,点P、Q分别在BD,AD上,则AP+PQ的最小值为( ) 
A.2 ![]()
B.![]()
C.2 ![]()
D.3 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线l1:y=x+3与x轴交于点A,与y轴交于点B,且与双曲线y= ![]() 交于点C(1,a).
交于点C(1,a).
(1)试确定双曲线的函数表达式;
(2)将l1沿y轴翻折后,得到l2 , 画出l2的图象,并求出l2的函数表达式;
(3)在(2)的条件下,点P是线段AC上点(不包括端点),过点P作x轴的平行线,分别交l2于点M,交双曲线于点N,求S△AMN的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E为边CD上一点,将△ADE沿AE折叠至△AD′E处,AD′与CE交于点F.若∠B=52°,∠DAE=20°,则∠FED′的大小为 . 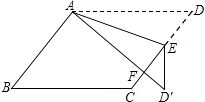
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一次数学课外实践活动中,小聪在距离旗杆10m的A处测得旗杆顶端B的仰角为60°,测角仪高AD为1m,则旗杆高BC为 m(结果保留根号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com