
【题目】如图,在矩形ABCD中,AD=6,AE⊥BD,垂足为E,ED=3BE,点P、Q分别在BD,AD上,则AP+PQ的最小值为( ) 
A.2 ![]()
B.![]()
C.2 ![]()
D.3 ![]()
【答案】D
【解析】解:
设BE=x,则DE=3x,
∵四边形ABCD为矩形,且AE⊥BD,
∴△ABE∽△DAE,
∴AE2=BEDE,即AE2=3x2 ,
∴AE= ![]() x,
x,
在Rt△ADE中,由勾股定理可得AD2=AE2+DE2 , 即62=( ![]() x)2+(3x)2 , 解得x=
x)2+(3x)2 , 解得x= ![]() ,
,
∴AE=3,DE=3 ![]() ,
,
如图,设A点关于BD的对称点为A′,连接A′D,PA′,
则A′A=2AE=6=AD,AD=A′D=6,
∴△AA′D是等边三角形,
∵PA=PA′,
∴当A′、P、Q三点在一条线上时,A′P+PQ最小,
又垂线段最短可知当PQ⊥AD时,A′P+PQ最小,
∴AP+PQ=A′P+PQ=A′Q=DE=3 ![]() ,
,
故选D.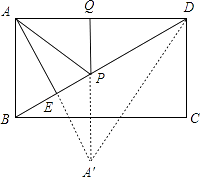
【考点精析】关于本题考查的矩形的性质和轴对称-最短路线问题,需要了解矩形的四个角都是直角,矩形的对角线相等;已知起点结点,求最短路径;与确定起点相反,已知终点结点,求最短路径;已知起点和终点,求两结点之间的最短路径;求图中所有最短路径才能得出正确答案.


 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案科目:初中数学 来源: 题型:
【题目】我国古代《易经》一书中记载,远古时期,人们通过在绳子上打结来记录数量,即“结绳计数”.如图,一位母亲在从右到左依次排列的绳子上打结,满七进一,用来记录孩子自出生后的天数,由图可知,孩子自出生后的天数是( )
A.84
B.336
C.510
D.1326
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是线段AB上的点,点C,D分别是线段OA,OB的中点,小明很轻松地求得CD=![]() AB.他在反思过程中突发奇想:若点O在线段AB的延长线上或在直线AB外,则原有的结论“CD=
AB.他在反思过程中突发奇想:若点O在线段AB的延长线上或在直线AB外,则原有的结论“CD=![]() AB”仍然成立吗?请帮小明解决此问题(当点O在线段AB的延长线上时,请画图分析该结论是否成立,并说明理由;当点O在直线AB外时,作出图形,通过度量说明该结论是否成立).
AB”仍然成立吗?请帮小明解决此问题(当点O在线段AB的延长线上时,请画图分析该结论是否成立,并说明理由;当点O在直线AB外时,作出图形,通过度量说明该结论是否成立).
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们规定:若 ![]() =(a,b),
=(a,b), ![]() =(c,d),则
=(c,d),则 ![]() =ac+bd.如
=ac+bd.如 ![]() =(1,2),
=(1,2), ![]() =(3,5),则
=(3,5),则 ![]() =1×3+2×5=13.
=1×3+2×5=13.
(1)已知 ![]() =(2,4),
=(2,4), ![]() =(2,﹣3),求
=(2,﹣3),求 ![]() ;
;
(2)已知 ![]() =(x﹣a,1),
=(x﹣a,1), ![]() =(x﹣a,x+1),求y=
=(x﹣a,x+1),求y= ![]() ,问y=
,问y= ![]() 的函数图象与一次函数y=x﹣1的图象是否相交,请说明理由.
的函数图象与一次函数y=x﹣1的图象是否相交,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数y= ![]() .
.
(1)若该反比例函数的图象与直线y=kx+4(k≠0)只有一个公共点,求k的值;
(2)如图,反比例函数y= ![]() (1≤x≤4)的图象记为曲线C1 , 将C1向左平移2个单位长度,得曲线C2 , 请在图中画出C2 , 并直接写出C1平移至C2处所扫过的面积.
(1≤x≤4)的图象记为曲线C1 , 将C1向左平移2个单位长度,得曲线C2 , 请在图中画出C2 , 并直接写出C1平移至C2处所扫过的面积. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,港口B位于港口O正西方向120km处,小岛C位于港口O北偏西60°的方向.一艘游船从港口O出发,沿OA方向(北偏西30°)以vkm/h的速度驶离港口O,同时一艘快艇从港口B出发,沿北偏东30°的方向以60km/h的速度驶向小岛C,在小岛C用1h加装补给物资后,立即按原来的速度给游船送去.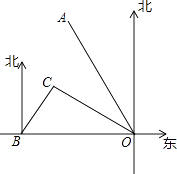
(1)快艇从港口B到小岛C需要多长时间?
(2)若快艇从小岛C到与游船相遇恰好用时1h,求v的值及相遇处与港口O的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com