
����Ŀ����ͼ��ʾ���ۿ�Bλ�ڸۿ�O��������120km����С��Cλ�ڸۿ�O��ƫ��60��ķ���һ���δ��Ӹۿ�O��������OA����ƫ��30�㣩��vkm/h���ٶ�ʻ��ۿ�O��ͬʱһ�ҿ�ͧ�Ӹۿ�B�������ر�ƫ��30��ķ�����60km/h���ٶ�ʻ��С��C����С��C��1h��װ�������ʺ�������ԭ�����ٶȸ��δ���ȥ��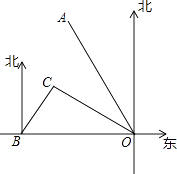
��1����ͧ�Ӹۿ�B��С��C��Ҫ�ʱ�䣿
��2������ͧ��С��C�����δ�����ǡ����ʱ1h����v��ֵ����������ۿ�O�ľ��룮
���𰸡�
��1��
�⣺�ߡ�CBO=60�㣬��COB=30�㣬
���BCO=90�㣮
��Rt��BCO����OB=120��
��BC= ![]() OB=60��
OB=60��
���ͧ�Ӹۿ�B��С��C��ʱ��Ϊ��60��60=1��Сʱ��
��2��
�⣺��C��CD��OA������ΪD������ᴦΪ��E��
��OC=OBcos30��=60 ![]() ��CD=
��CD= ![]() OC=30
OC=30 ![]() ��OD=OCcos30��=90��
��OD=OCcos30��=90��
��DE=90��3v��
��CE=60��CD2+DE2=CE2��
�ࣨ30 ![]() ��2+��90��3v��2=602��
��2+��90��3v��2=602��
��v=20��40��
�൱v=20km/hʱ��OE=3��20=60km��
��v=40km/hʱ��OE=3��40=120km��
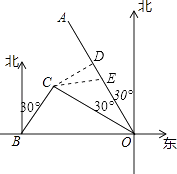
����������1��Ҫ��B��C��ʱ�䣬��֪���ٶȣ���ֻҪ���BC��·�̣�������·�̹�ʽ������������ʱ�䣻��2����C��CD��OA������ΪD������ᴦΪ��E�����OC=OBcos30��=60 ![]() ��CD=
��CD= ![]() OC=30
OC=30 ![]() ��OD=OCcos30��=90����DE=90��3v����ֱ�ǡ�CDE�����ù��ɶ����ó�CD2+DE2=CE2 �� ����30
��OD=OCcos30��=90����DE=90��3v����ֱ�ǡ�CDE�����ù��ɶ����ó�CD2+DE2=CE2 �� ����30 ![]() ��2+��90��3v��2=602 �� �ⷽ�����v=20��40�����������������ۿ�O�ľ��룮
��2+��90��3v��2=602 �� �ⷽ�����v=20��40�����������������ۿ�O�ľ��룮


 ��ʦ�㾦�ִʾ��ƪϵ�д�
��ʦ�㾦�ִʾ��ƪϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У�AD=6��AE��BD������ΪE��ED=3BE����P��Q�ֱ���BD��AD�ϣ���AP+PQ����СֵΪ�� �� 
A.2 ![]()
B.![]()
C.2 ![]()
D.3 ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ǭ������ij��ѧΪ�˽ⱾУѧ��ƽ��ÿ��Ŀ���ѧϰʵ������������ȡ����ѧ�������ʾ����飬������������ΪA��B��C��D�ĸ��ȼ�����ѧ��ʱ��Ϊt��Сʱ����A��t��1��B��1��t��1.5��C��1.5��t��2��D��t��2�����ݵ�������������ͼ��ʾ��������������ͳ��ͼ���������ͼ����Ϣ����������⣺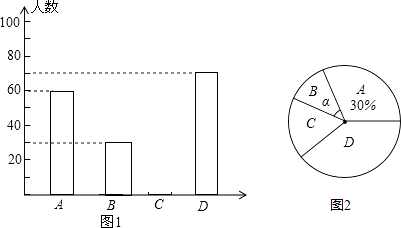
��1�����γ������鹲��ȡ�˶�����ѧ������������ͳ��ͼ����������
��2�����γ��������У�ѧϰʱ�����λ�������ĸ��ȼ��ڣ�
��3����ʾB�ȼ�������Բ�ĽǦ��Ķ����Ƕ��٣�
��4���ڴ˴��ʾ������У��װ���2��ƽ��ÿ�����ѧϰʱ�䳬��2Сʱ���Ұ���3��ƽ��ÿ�����ѧϰʱ�䳬��2Сʱ��������5������ѡ2��ȥ�μ���̸�������б�����״ͼ�ķ�����ѡ����2�����Բ�ͬ�༶�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڹ���Ժ�칫���������й�����չ�ĸ����巽����֮��ijУΪ�˵��鱾Уѧ��������֪ʶ���˽�̶ȣ������ȡ�˲���ѧ������һ���ʾ����飬�����ݵ�������������ͼ��ͳ��ͼ�������ͼ����������Ϣ������������⣺
��1�����ν����ʾ������ѧ������������
��2������ͳ��ͼ�У����˽⡱����Ӧ���ε�Բ�ĽǵĶ���Ϊ �� m��ֵΪ��
��3������У����ѧ��1500������������������������Уѧ����������˽�̶�Ϊ�������˽⡱��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ����ѧ����ʵ����У�С���ھ������10m��A�������˶���B������Ϊ60�㣬����Ǹ�ADΪ1m������˸�BCΪ m������������ţ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ۺ��⡣
��1�����㣺2��1+��2�Щ�1��0�� ![]() ��sin45�㩁
��sin45�㩁 ![]() tan30��
tan30��
��2���ⷽ�̣�x2+4x��1=0��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С�µ�һ����һö�ʵؾ��ȵ�Ӳ��ʱ�������ϣ����ڶ���������öӲ��ʱ���������ϵĸ����� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�O��ֱ������C�ǡ�O��һ�㣬AD�����C�����ߴ�ֱ������Ϊ��D��ֱ��DC��AB���ӳ����ཻ�ڵ�P��CEƽ�֡�ACB����AB�ڵ�E��
��1����֤��ACƽ�֡�DAB��
��2����֤����PCE�ǵ��������Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y=x��1�뷴��������y= ![]() ��ͼ����A��B���㣬��x�ύ�ڵ�C����֪��A������Ϊ����1��m����
��ͼ����A��B���㣬��x�ύ�ڵ�C����֪��A������Ϊ����1��m���� 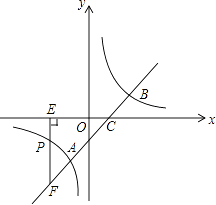
��1�����������Ľ���ʽ��
��2������P��n����1���Ƿ���������ͼ����һ�㣬����P��PE��x���ڵ�E���ӳ�EP��ֱ��AB�ڵ�F�����CEF�������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com