
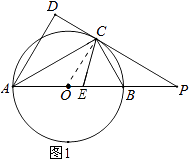
【题目】如图,AB是⊙O的直径,点C是⊙O上一点,AD与过点C的切线垂直,垂足为点D,直线DC与AB的延长线相交于点P,CE平分∠ACB,交AB于点E.
(1)求证:AC平分∠DAB;
(2)求证:△PCE是等腰三角形.
【答案】
(1)
解:如图1所示:连接OC.
∵PD切⊙O于点C,
∴OC⊥PD.
又∵AD⊥PD,
∴OC∥AD.
∴∠ACO=∠DAC.
又∵OC=OA,
∴∠ACO=∠CAO,
∴∠DAC=∠CAO,
即AC平分∠DAB
(2)
解:∵AD⊥PD,
∴∠DAC+∠ACD=90°.
又∵AB为⊙O的直径,
∴∠ACB=90°.
∴∠PCB+∠ACD=90°,
∴∠DAC=∠PCB.
又∵∠DAC=∠CAO,
∴∠CAO=∠PCB.
∵CE平分∠ACB,
∴∠ACE=∠BCE,
∴∠CAO+∠ACE=∠PCB+∠BCE,
∴∠PEC=∠PCE,
∴PC=PE,
即△PCE是等腰三角形
【解析】(1)依据切线的性质可知OC⊥DC,然后可证明AD∥OC,依据平行线的性质可得到∠DAC=∠ACO,然后依据OA=OC可证明∠OAC=∠ACO,通过等量代换可证明AC平分∠DAB;(2)依据直径所对的圆周角等于90°可证明∠ACB=90°,然后依据同角的余角相等可证明∠DAC=∠BCP,由(1)可知AC平分∠DAB,从而得到∠CAE=∠BCP,然后结合∠ACE=∠ECB可证明∠PCE=∠PEC.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:
【题目】已知反比例函数y= ![]() .
.
(1)若该反比例函数的图象与直线y=kx+4(k≠0)只有一个公共点,求k的值;
(2)如图,反比例函数y= ![]() (1≤x≤4)的图象记为曲线C1 , 将C1向左平移2个单位长度,得曲线C2 , 请在图中画出C2 , 并直接写出C1平移至C2处所扫过的面积.
(1≤x≤4)的图象记为曲线C1 , 将C1向左平移2个单位长度,得曲线C2 , 请在图中画出C2 , 并直接写出C1平移至C2处所扫过的面积. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,港口B位于港口O正西方向120km处,小岛C位于港口O北偏西60°的方向.一艘游船从港口O出发,沿OA方向(北偏西30°)以vkm/h的速度驶离港口O,同时一艘快艇从港口B出发,沿北偏东30°的方向以60km/h的速度驶向小岛C,在小岛C用1h加装补给物资后,立即按原来的速度给游船送去.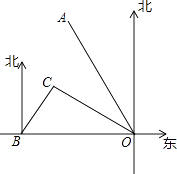
(1)快艇从港口B到小岛C需要多长时间?
(2)若快艇从小岛C到与游船相遇恰好用时1h,求v的值及相遇处与港口O的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将线段AB绕点O顺时针旋转90°得到线段A′B′,那么A(﹣2,5)的对应点A′的坐标是( )
A.(2,5)
B.(5,2)
C.(4, ![]() )
)
D.( ![]() ,4)
,4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】冬天来了,晒衣服成了头疼的事情,聪明的小华想到一个好办法,在家后院地面(BD)上立两根等长的立柱AB、CD(均与地面垂直),并在立柱之间悬挂一根绳子.由于挂的衣服比较多,绳子的形状近似成了抛物线y=ax2﹣0.8x+c,如图1,已知立柱AB=CD=2.6米,BD=8米. 
(1)求绳子最低点离地面的距离;
(2)为了防止衣服碰到地面,小华在离AB为3米的位置处用一根垂直于地面的立柱MN撑起绳子(如图2),使左边抛物线F1的最低点距MN为1米,离地面1.6米,求MN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年3月,我市某中学举行了“爱我中国朗诵比赛”活动,根据学生的成绩划分为A、B、C、D四个等级,并绘制了不完整的两种统计图.根据图中提供的信息,回答下列问题:
(1)参加朗诵比赛的学生共有人,并把条形统计图补充完整理;
(2)扇形统计图中,m= , n=;C等级对应扇形有圆心角为度;
(3)学校欲从获A等级的学生中随机选取2人,参加市举办的朗诵比赛,请利用列表法或树形图法,求获A等级的小明参加市朗诵比赛的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】盐城市“创建文明城市”活动如火如荼的展开.某中学为了搞好“创建文明城市”活动的宣传,校学生会就本校学生对盐城“市情市况”的了解程度进行了一次调查测试.经过对测试成绩的分析,得到如下图所示的两幅不完整的统计图(A:59分及以下;B:60﹣69分;C:70﹣79分;D:80﹣89分;E:90﹣100分).请你根据图中提供的信息解答以下问题: 
(1)求该校共有多少名学生;
(2)将条形统计图补充完整;
(3)在扇形统计图中,计算出“60﹣69分”部分所对应的圆心角的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com