
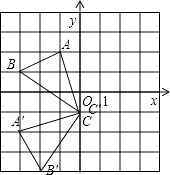
【题目】如图,若将△ABC绕点C逆时针旋转90°后得到△A′B′C′,
(1)在图中画出△A′B′C′;
(2)求出点A经过的路径长.
【答案】
(1)
解:如图,△A′B′C′为所作;
(2)
解:AC= ![]() =
= ![]() ,
,
所以点A经过的路径长= ![]() =
= ![]() π
π
【解析】(1)利用网格特点和旋转的性质画出点A、B的对应点A′、B′,从而得到△A′B′C′,(2)点A经过的路径为以点C为圆心,CA为半径,圆心角为90°的弧,则根据弧长公式可计算出点A经过的路径长.
【考点精析】根据题目的已知条件,利用弧长计算公式和旋转的性质的相关知识可以得到问题的答案,需要掌握若设⊙O半径为R,n°的圆心角所对的弧长为l,则l=nπr/180;注意:在应用弧长公式进行计算时,要注意公式中n的意义.n表示1°圆心角的倍数,它是不带单位的;①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O(0,0),A(0,﹣6),B(8,0)三点在⊙P上.
(1)求圆的半径及圆心P的坐标;
(2)M为劣弧 ![]() 的中点,求证:AM是∠OAB的平分线;
的中点,求证:AM是∠OAB的平分线;
(3)连接BM并延长交y轴于点N,求N,M点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在国务院办公厅发布《中国足球发展改革总体方案》之后,某校为了调查本校学生对足球知识的了解程度,随机抽取了部分学生进行一次问卷调查,并根据调查结果绘制了如图的统计图,请根据图中所给的信息,解答下列问题:
(1)本次接受问卷调查的学生总人数是;
(2)扇形统计图中,“了解”所对应扇形的圆心角的度数为 , m的值为;
(3)若该校共有学生1500名,请根据上述调查结果估算该校学生对足球的了解程度为“基本了解”的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C是⊙O上一点,AD与过点C的切线垂直,垂足为点D,直线DC与AB的延长线相交于点P,CE平分∠ACB,交AB于点E.
(1)求证:AC平分∠DAB;
(2)求证:△PCE是等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋中装有4个分别标有数1,2,3,4的小球,它们的形状、大小完全相同,小红先从口袋里随机摸出一个小球记下数为x,小颖在剩下的3个球中随机摸出一个小球记下数为y,这样确定了点P的坐标(x,y).
(1)小红摸出标有数3的小球的概率是 .
(2)请你用列表法或画树状图法求点P(x,y)在函数y=﹣x+5图象上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD是正方形,E、F分别是DC和CB的延长线上的点,且DE=BF,连接AE、AF、EF. 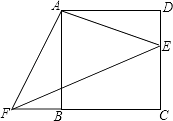
(1)求证:△ADE≌△ABF;
(2)若BC=8,DE=6,求△AEF的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com