
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 是斜边
是斜边![]() 上两点,且
上两点,且![]() ,若
,若![]() ,
,![]() ,则
,则![]() 的长为__.
的长为__.

【答案】![]()
【解析】
过点B作边BC的垂线截取BF=DC=3,即可构造出两直角边分别为3和4,斜边为5的直角三角形,连接AF易证明△AFB≌△ADC,连接FE易证明△AFE≌△ADE,从而求得DE=EF=5,进而求得BC的长,再根据△ABC是等腰直角三角形,利用三角函数易求得AB的长.
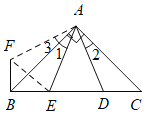
解:如图过B作BC的垂线,垂足为B,并截取BF=CD,连接FE,AF.
∵∠FBE=90°,FB=3,BE=4
∴在Rt△FBE中,FE2=FB2+BE2=32+42=52
∴FE=5
又∵AB=AC,∠BAC=90°,
∴Rt△ABC是等腰直角三角形,
∴∠ABC=∠ACB=45°,
∴∠FBA=∠FBC-∠ABC=90°-45°=45°,
∴∠FBA=∠ACB,
在△AFB与△ADC中
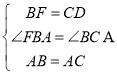 ∴△AFB≌△ADC(SAS)
∴△AFB≌△ADC(SAS)
∴∠2=∠3,AF=AD
又∵∠1+∠EAD+∠2=90°,![]()
∴∠1+∠2=45°
∴∠FAE=∠1+∠3=∠1+∠2=45°
∴∠FAE=∠DAE
∴在△AFE与△ADE中
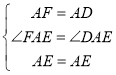
∴△AFE≌△ADE(SAS)
∴FE=DE=5
∴BC=BE+ED+DC=4+5+3=12
又∵在Rt△ABC中AB= BC cos∠ABC
即AB=12×cos45°=![]() 12=6
12=6![]() .
.
故答案为:6![]() .
.


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:初中数学 来源: 题型:
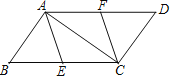
【题目】已知点E、F分别是ABCD的边BC、AD的中点.
(1)求证:四边形AECF是平行四边形;
(2)若BC=10,∠BAC=90°,求AECF的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了节能减排,我市某校准备购买某种品牌的节能灯,已知3只A型节能灯和5只B型节能灯共需50元,2只A型节能灯和3只B型节能灯共需31元.
(1)求1只A型节能灯和1只B型节能灯的售价各是多少元?
(2)学校准备购买这两种型号的节能灯共200只,要求A型节能灯的数量不超过B型节能灯的数量的3倍,请设计出最省钱的购买方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校计划组织全校1441名师生到相关部门规划的林区植树,经过研究,决定租用当地租车公司一共62辆![]() 两种型号客车作为交通工具.
两种型号客车作为交通工具.
下表是租车公司提供给学校有关两种型号客车的载客量和租金信息:
型号 | 载客量 | 租金单价 |
| 30人/辆 | 380元/辆 |
| 20人/辆 | 280元/辆 |
注:载客量指的是每辆客车最多可载该校师生的人数.设学校租用![]() 型号客车
型号客车![]() 辆,租车总费用为
辆,租车总费用为![]() 元.
元.
(1)求![]() 与
与![]() 的函数解析式,请直接写出
的函数解析式,请直接写出![]() 的取值范围;
的取值范围;
(2)若要使租车总费用不超过21940元,一共有几种租车方案?哪种租车方案总费用最省?最省的总费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
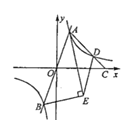
【题目】如图,过原点的直线与反比例函数![]() 的图象交于
的图象交于![]() ,
,![]() 两点,点
两点,点![]() 在第一象限点
在第一象限点![]() 在
在![]() 轴正半轴上,连结
轴正半轴上,连结![]() 交反比例函数图象于点
交反比例函数图象于点![]() .
.![]() 为
为![]() 的平分线,过点
的平分线,过点![]() 作
作![]() 的垂线,垂足为
的垂线,垂足为![]() ,连结
,连结![]() .若
.若![]() ,
,![]() 的面积为8,则
的面积为8,则![]() 的值为________.
的值为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
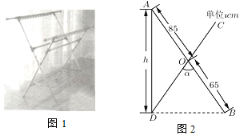
【题目】有一种落地晾衣架如图1所示,其原理是通过改变两根支撑杆夹角的度数来调整晾衣杆的高度. 图2是支撑杆的平面示意图,AB和CD分别是两根不同长度的支撑杆,夹角∠BOD=![]() . 若AO=85cm,BO=DO=65cm. 问: 当
. 若AO=85cm,BO=DO=65cm. 问: 当![]() ,较长支撑杆的端点
,较长支撑杆的端点![]() 离地面的高度
离地面的高度![]() 约为_____
约为_____![]() .(参考数据:
.(参考数据:![]()
![]() ,
,![]() .)
.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,O为坐标原点,点A(4,0),以OA为对角线作正方形ABOC,若将抛物线y=![]() x2沿射线OC平移得到新抛物线y=
x2沿射线OC平移得到新抛物线y=![]() (x-m)2+k(m>0).则当新抛物线与正方形的边AB有公共点时,m的值一定是( )
(x-m)2+k(m>0).则当新抛物线与正方形的边AB有公共点时,m的值一定是( )
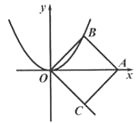
A. 2,6,8B. 0<m≤6C. 0<m≤8D. 0<m≤2或 6 ≤ m≤8
查看答案和解析>>
科目:初中数学 来源: 题型:
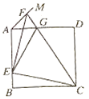
【题目】如图,正方形ABCD的边长为a,点E在边AB上运动(不与点A,B重合),∠DAM=45°,点F在射线AM上,且![]() ,CF与AD相交于点G,连接EC,EF,EG,则下列结论:①∠ECF=45°;②
,CF与AD相交于点G,连接EC,EF,EG,则下列结论:①∠ECF=45°;②![]() 的周长为
的周长为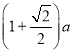 ;③
;③![]() ;④
;④![]() 的面积的最大值
的面积的最大值![]() .其中正确的结论是____.(填写所有正确结论的序号)
.其中正确的结论是____.(填写所有正确结论的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com