
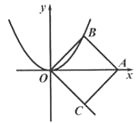
【题目】如图,在直角坐标系中,O为坐标原点,点A(4,0),以OA为对角线作正方形ABOC,若将抛物线y=![]() x2沿射线OC平移得到新抛物线y=
x2沿射线OC平移得到新抛物线y=![]() (x-m)2+k(m>0).则当新抛物线与正方形的边AB有公共点时,m的值一定是( )
(x-m)2+k(m>0).则当新抛物线与正方形的边AB有公共点时,m的值一定是( )
A. 2,6,8B. 0<m≤6C. 0<m≤8D. 0<m≤2或 6 ≤ m≤8
【答案】D
【解析】
根据正方形的性质得出∠AOC=45°,B(2,2),根据第四象限角平分线上的点的横坐标与纵坐标互为相反数及平移的规律和方向得出新抛物线的解析式为y=![]() (x-m)2-m,然后将A,B两点的坐标分别代入即可求出m的值,根据抛物线的性质从而求出m的取值范围
(x-m)2-m,然后将A,B两点的坐标分别代入即可求出m的值,根据抛物线的性质从而求出m的取值范围
∵ 点A(4,0) ,
∴OA=4,
∵ OA为正方形ABOC对角线,
∴∠AOC=45°,B(2,2),
∴直线OC上所有点的横坐标与纵坐标互为相反数,
∵ 将抛物线y=![]() x2沿射线OC平移得到新抛物线y=
x2沿射线OC平移得到新抛物线y=![]() (x-m)2+k(m>0) ,
(x-m)2+k(m>0) ,
∴该新抛物线的顶点坐标一定在直线OC上,
∴该新抛物线的顶点坐标是(m,-m),即新抛物线为y= ![]() (x-m)2-m; ,将点B(2,2)代入得
(x-m)2-m; ,将点B(2,2)代入得 ![]() (2-m)2-m=2,解得 m1=0,m2=6;将点A(4,0)代入得
(2-m)2-m=2,解得 m1=0,m2=6;将点A(4,0)代入得 ![]() (4-m)2-m=0,解得 m3=2,m4=6;
(4-m)2-m=0,解得 m3=2,m4=6;
∴在平移的过程中新抛物线与正方形的边AB有公共点 时,m的值为 0<m≤2 或 6 ≤ m≤8
故答案为:D.


科目:初中数学 来源: 题型:
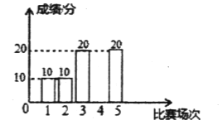
【题目】冰雪之王总决赛(以下简称“雪合战”)在我市落下帷幕.已知不同小组的甲、乙两队的五次预选赛成绩分别如下列不完整的统计表及统计图所示(每次比赛的成绩为0分,10分,20分三种情况).
甲队五次预选赛成绩统计表
比赛场次 | 1 | 2 | 3 | 4 | 5 |
成绩(分) | 20 | 0 | 20 |
| 20 |
已知甲、乙两队五次预选赛成绩的众数相同,平均数也相同.
(1)补全条形统计图;
(2)求甲队成绩的平均数及![]() 的值;
的值;
(3)从甲、乙两队前3次比赛中随机各选一场比赛的成绩进行比较,求选择到的甲队成绩优于乙队成绩的概率.
乙队五次预选赛成绩条形统计图
查看答案和解析>>
科目:初中数学 来源: 题型:
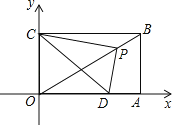
【题目】矩形OABC在平面直角坐标系中的位置如图所示,已知![]() ,点A在x轴上,点C在y轴上,P是对角线OB上一动点(不与原点重合),连接PC,过点P作
,点A在x轴上,点C在y轴上,P是对角线OB上一动点(不与原点重合),连接PC,过点P作![]() ,交x轴于点D.下列结论:①
,交x轴于点D.下列结论:①![]() ;②当点D运动到OA的中点处时,
;②当点D运动到OA的中点处时,![]() ;③在运动过程中,
;③在运动过程中,![]() 是一个定值;④当△ODP为等腰三角形时,点D的坐标为
是一个定值;④当△ODP为等腰三角形时,点D的坐标为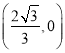 .其中正确结论的个数是( )
.其中正确结论的个数是( )
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 的图象过点
的图象过点![]() .
.
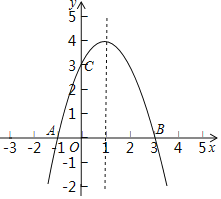
(1)求抛物线的解析式;
(2)在抛物线的对称轴上是否存在一点P,使得△PAC的周长最小,若存在,请求出点P的坐标及△PAC的周长;若不存在,请说明理由;
(3)在(2)的条件下,在x轴上方的抛物线上是否存在点M(不与C点重合),使得![]() ?若存在,请求出点M的坐标;若不存在,请说明理由.
?若存在,请求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,抛物线y=x2+2mx(m为常数且m≠0).
(1)判断该抛物线与x轴的交点个数,并说明理由.
(2)若点A(-n+5,0),B(n-1,0)在该抛物线上,点M为抛物线的顶点,求△ABM的面积.
(3)若点(2,p),(3,g),(4,r)均在该抛物线上,且p<g<r,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在![]() 中,
中,![]() ,
,![]() 是
是![]() 的外接圆,过点
的外接圆,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,延长
,延长![]() 至点
至点![]() ,使
,使![]() ,连接
,连接![]() .
.
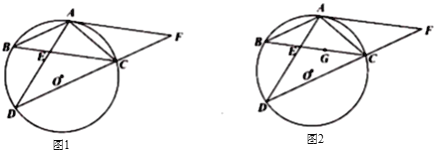
(1)求证:![]() ;
;
(2)求证:![]() 是
是![]() 的切线;
的切线;
(3)如图2,若点![]() 是
是![]() 的内心,
的内心,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,矩形![]() 中,
中,![]() ,点
,点![]() 分别在边
分别在边![]() 上,直线
上,直线![]() 交矩形对角线
交矩形对角线![]() 于点
于点![]() ,将
,将![]() 沿直线
沿直线![]() 翻折,点
翻折,点![]() 落在点
落在点![]() 处,且点
处,且点![]() 在射线
在射线![]() 上。
上。
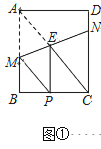

Ⅰ.如图①,当![]() 时,①求证
时,①求证![]() ;②求
;②求![]() 的长;
的长;
Ⅱ.请写出线段![]() 的长的取值范围,及当
的长的取值范围,及当![]() 的长最大时
的长最大时![]() 的长。
的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一段抛物线y=-x(x-5)(0≤x≤5),记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x轴于点A2;将C2绕点A2旋转180°得C3,交x轴于点A3;…如此进行下去,若P(2 017,m)是其中某段抛物线上一点,则m为( )
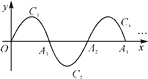
A. 4B. -4C. -6D. 6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com