
【题目】已知,矩形![]() 中,
中,![]() ,点
,点![]() 分别在边
分别在边![]() 上,直线
上,直线![]() 交矩形对角线
交矩形对角线![]() 于点
于点![]() ,将
,将![]() 沿直线
沿直线![]() 翻折,点
翻折,点![]() 落在点
落在点![]() 处,且点
处,且点![]() 在射线
在射线![]() 上。
上。
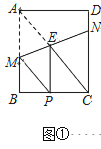

Ⅰ.如图①,当![]() 时,①求证
时,①求证![]() ;②求
;②求![]() 的长;
的长;
Ⅱ.请写出线段![]() 的长的取值范围,及当
的长的取值范围,及当![]() 的长最大时
的长最大时![]() 的长。
的长。
【答案】Ⅰ. ①见解析;②![]() ;Ⅱ.0≤CP≤5,
;Ⅱ.0≤CP≤5,![]()
【解析】
Ⅰ. ①先由折叠得出∠AEM=∠PEM,AE=PE,再根据已知判断出AB∥EP,进而判断出CN=CE,②设CN=CE=x,先根据勾股定理求出AC的长,再根据AB∥EP证出![]() CPE
CPE![]() CAB,从而得到比例式即可.
CAB,从而得到比例式即可.
Ⅱ. 先确定出PC最大和最小时的位置,即可得出PC的范围,最后用折叠的性质和勾股定理即可得出结论.
解:Ⅰ. ①∵△AME沿直线MN翻折,点A落在点P处,
∴△AME≌△PME.
∴∠AEM=∠PEM,AE=PE.
∵ABCD是矩形,∴AB⊥BC.
∵EP⊥BC,∴AB∥EP.
∴∠AME=∠PEM.
∴∠AEM=∠AME.
∴AM=AE,
∵ABCD是矩形,∴AB∥DC.
∴![]() .∴CN=CE,
.∴CN=CE,
②设CN=CE=x.
∵ABCD是矩形,AB=4,BC=3,
∴根据勾股定理得AC=5.∴PE=AE=5-x.
∵EP⊥BC,AB∥EP
∴![]() CPE
CPE![]() CAB
CAB
∴![]() =
=![]() =
=![]() .
.
∴![]() ,
,
∴x=![]() ,
,
即CN=![]()
Ⅱ. ∵四边形ABCD是矩形,
∴∠ABC=90°,AC=5,
由折叠知,AE=PE,
由三角形的三边关系得,PE+CE>PC,
∴AC>PC,
∴PC<5,
∴点E是AC中点时,PC最小为0,当点E和点C重合时,PC最大为AC=5,
∴0≤CP≤5,
如图,当点C,N,E重合时,PC=BC+BP=5,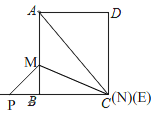
∴BP=2,
由折叠知,PM=AM,
在Rt△PBM中,PM=4-BM,根据勾股定理得,PM2-BM2=BP2,
∴(4-BM)2-BM2=4,
∴BM=![]() ,
,
在Rt△BCM中,根据勾股定理得,MN=
当CP最大时MN=![]() ,
,


科目:初中数学 来源: 题型:
【题目】为了节能减排,我市某校准备购买某种品牌的节能灯,已知3只A型节能灯和5只B型节能灯共需50元,2只A型节能灯和3只B型节能灯共需31元.
(1)求1只A型节能灯和1只B型节能灯的售价各是多少元?
(2)学校准备购买这两种型号的节能灯共200只,要求A型节能灯的数量不超过B型节能灯的数量的3倍,请设计出最省钱的购买方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,O为坐标原点,点A(4,0),以OA为对角线作正方形ABOC,若将抛物线y=![]() x2沿射线OC平移得到新抛物线y=
x2沿射线OC平移得到新抛物线y=![]() (x-m)2+k(m>0).则当新抛物线与正方形的边AB有公共点时,m的值一定是( )
(x-m)2+k(m>0).则当新抛物线与正方形的边AB有公共点时,m的值一定是( )
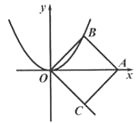
A. 2,6,8B. 0<m≤6C. 0<m≤8D. 0<m≤2或 6 ≤ m≤8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织学生参加“安全知识竞赛”(满分为![]() 分),测试结束后,张老师从七年级
分),测试结束后,张老师从七年级![]() 名学生中随机地抽取部分学生的成绩绘制了条形统计图,如图
名学生中随机地抽取部分学生的成绩绘制了条形统计图,如图![]() 所示.试根据统计图提供的信息,回答下列问题:
所示.试根据统计图提供的信息,回答下列问题:
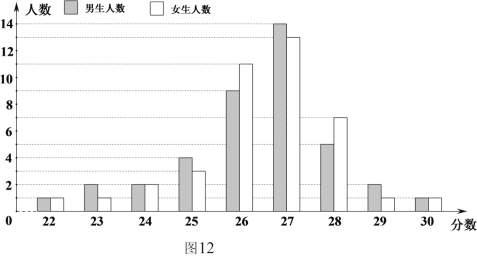
(1)张老师抽取的这部分学生中,共有 名男生, 名女生;
(2)张老师抽取的这部分学生中,女生成绩的众数是 ;
(3)若将不低于![]() 分的成绩定为优秀,请估计七年级
分的成绩定为优秀,请估计七年级![]() 名学生中成绩为优秀的学生人数大约是多少.
名学生中成绩为优秀的学生人数大约是多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组![]() 请结合题意填空,完成本题的解答、
请结合题意填空,完成本题的解答、
(I)解不等式①,得
(II)解不等式②,得
(III)把不等式①和②的解集在数轴上表示出来:
![]()
(IV)原不等式组的解集为
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ,
,![]() 为常数)的图象经过点
为常数)的图象经过点![]() .
.
(1)求![]() ,
,![]() 满足的关系式;
满足的关系式;
(2)设该函数图象的顶点坐标是![]() ,当
,当![]() 的值变化时,求
的值变化时,求![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(3)若该函数的图象不经过第三象限,当![]() 时,函数的最大值与最小值之差为16,求
时,函数的最大值与最小值之差为16,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
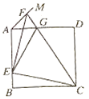
【题目】如图,正方形ABCD的边长为a,点E在边AB上运动(不与点A,B重合),∠DAM=45°,点F在射线AM上,且![]() ,CF与AD相交于点G,连接EC,EF,EG,则下列结论:①∠ECF=45°;②
,CF与AD相交于点G,连接EC,EF,EG,则下列结论:①∠ECF=45°;②![]() 的周长为
的周长为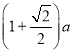 ;③
;③![]() ;④
;④![]() 的面积的最大值
的面积的最大值![]() .其中正确的结论是____.(填写所有正确结论的序号)
.其中正确的结论是____.(填写所有正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】给出以下命题:
①平分弦的直径垂直于这条弦;
②已知点![]() 、
、![]() 、
、![]() 均在反比例函数
均在反比例函数![]() 的图象上,则
的图象上,则![]() ;
;
③若关于x的不等式组![]() 无解,则
无解,则![]() ;
;
④将点![]() 向左平移3个单位到点
向左平移3个单位到点![]() ,再将
,再将![]() 绕原点逆时针旋转90°到点
绕原点逆时针旋转90°到点![]() ,则
,则![]() 的坐标为
的坐标为![]() .
.
其中所有真命题的序号是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,二次函数的图像交坐标轴于A(-1,0),B(4,0),C(0,-4)三点,点P是直线BC下方抛物线上一动点.

(1)求这个二次函数的解析式;
(2)是否存在点P,使△POC是以OC为底边的等腰三角形?若存在,求出P点坐标;若不存在,请说明理由;
(3)动点P运动到什么位置时,△PBC面积最大,求出此时P点坐标和△PBC的最大面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com