
【题目】如图,在平面直角坐标系中,二次函数的图像交坐标轴于A(-1,0),B(4,0),C(0,-4)三点,点P是直线BC下方抛物线上一动点.

(1)求这个二次函数的解析式;
(2)是否存在点P,使△POC是以OC为底边的等腰三角形?若存在,求出P点坐标;若不存在,请说明理由;
(3)动点P运动到什么位置时,△PBC面积最大,求出此时P点坐标和△PBC的最大面积.
【答案】(1)![]()
(2)存在,P(![]() )
)
(3)当P点位(2,-6)时,最大面积为8
【解析】
(1)由A、B、C三点的坐标,利用待定系数法可求得抛物线解析式;
(2)由题意可知点P在线段OC的垂直平分线上,则可求得P点纵坐标,代入抛物线解析式可求得P点坐标;
(3)过P作PE⊥x轴,交x轴于点E,交直线BC于点F,用P点坐标可表示出PF的长,则可表示出△PBC的面积,利用二次函数的性质可求得△PBC面积的最大值及P点的坐标.
(1)设抛物线解析式为![]()
把A. B. C三点坐标代入可得 解得
解得
∴抛物线解析式为![]()
(2)作OC的垂直平分线DP,交OC于点D,交BC下方抛物线于点P,如图1,

∴PO=PD,此时P点即为满足条件的点,
∵C(0,4),
∴D(0,2),
∴P点纵坐标为2,
代入抛物线解析式可得![]() ,解得
,解得![]() (小于0,舍去)或
(小于0,舍去)或![]() ∴存在满足条件的P点,其坐标为
∴存在满足条件的P点,其坐标为
(3)∵点P在抛物线上,
∴可设P![]() ,
,
过P作PE⊥x轴于点E,交直线BC于点F,如图2,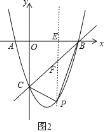
∵B(4,0),C(0,4),
∴直线BC解析式为y=x4,
∴F(t,t4),
∴![]()
∴S![]() =S
=S![]() +S
+S![]() =
=![]() PFOE+
PFOE+![]() PFBE=
PFBE=![]() PF(OE+BE)
PF(OE+BE)
=![]() PFOB
PFOB![]()
![]() ×4=2(t2)2+8,
×4=2(t2)2+8,
∴当t=2时,S![]() 最大值为8,此时t
最大值为8,此时t![]() 3t4=6,
3t4=6,
∴当P点坐标为(2,6)时,△PBC的最大面积为8.


科目:初中数学 来源: 题型:
【题目】已知,矩形![]() 中,
中,![]() ,点
,点![]() 分别在边
分别在边![]() 上,直线
上,直线![]() 交矩形对角线
交矩形对角线![]() 于点
于点![]() ,将
,将![]() 沿直线
沿直线![]() 翻折,点
翻折,点![]() 落在点
落在点![]() 处,且点
处,且点![]() 在射线
在射线![]() 上。
上。
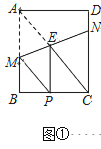

Ⅰ.如图①,当![]() 时,①求证
时,①求证![]() ;②求
;②求![]() 的长;
的长;
Ⅱ.请写出线段![]() 的长的取值范围,及当
的长的取值范围,及当![]() 的长最大时
的长最大时![]() 的长。
的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一段抛物线y=-x(x-5)(0≤x≤5),记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x轴于点A2;将C2绕点A2旋转180°得C3,交x轴于点A3;…如此进行下去,若P(2 017,m)是其中某段抛物线上一点,则m为( )
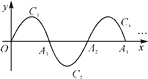
A. 4B. -4C. -6D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在函数![]() 的图象上有点
的图象上有点![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,点
,点![]() 的横坐标为2,且后面每个点的横坐标与它前面相邻点的横坐标的差都是2,过点
的横坐标为2,且后面每个点的横坐标与它前面相邻点的横坐标的差都是2,过点![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 分别作
分别作![]() 轴、
轴、![]() 轴的垂线段,构成若干个矩形,如图所示,将图中阴影部分的面积从左至右依次记为
轴的垂线段,构成若干个矩形,如图所示,将图中阴影部分的面积从左至右依次记为![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() .则
.则![]() ________,
________,![]() ________.(用含
________.(用含![]() 的代数式表示)
的代数式表示)
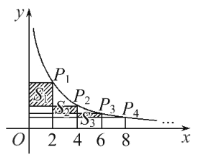
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 与x轴的2个交点间的距离为4不单位长度,其顶点在第二象限下列结论;①a<0;②抛物线的对称轴为直线
与x轴的2个交点间的距离为4不单位长度,其顶点在第二象限下列结论;①a<0;②抛物线的对称轴为直线![]() ,③当
,③当![]() 时,y的值随x值的增大而减小;④
时,y的值随x值的增大而减小;④![]() 。其中正确的有( )
。其中正确的有( )
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
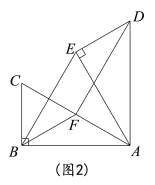
【题目】在Rt△ABC中,∠ABC=90°,∠BAC=30°,将△ABC绕点A顺时针旋转一定的角度![]() 得到△AED,点B、C的对应点分别是E、D.
得到△AED,点B、C的对应点分别是E、D.
(1)如图1,当点E恰好在AC上时,求∠CDE的度数;
(2)如图2,若![]() =60°时,点F是边AC中点,求证:四边形BFDE是平行四边形.
=60°时,点F是边AC中点,求证:四边形BFDE是平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
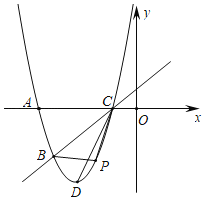
【题目】如图,已知抛物线![]() 经过
经过![]() ,
,![]() 两点,与x轴的另一个交点为C,顶点为D,连结CD.
两点,与x轴的另一个交点为C,顶点为D,连结CD.
(1)求该抛物线的表达式;
(2)点P为该抛物线上一动点(与点B、C不重合),设点P的横坐标为t.
①当点P在直线BC的下方运动时,求![]() 的面积的最大值;
的面积的最大值;
②该抛物线上是否存在点P,使得![]() 若存在,求出所有点P的坐标;若不存在,请说明理由.
若存在,求出所有点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
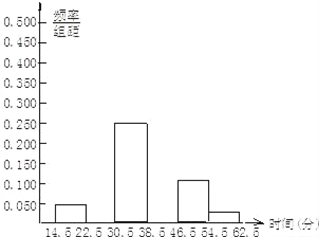
【题目】某校为了了解全校400名学生参加课外锻炼的情况,随机对40名学生一周内平均每天参加课外锻炼的时间进行了调查,结果如下:(单位:分)
40 21 35 24 40 38 23 52 35 62 36 15 51 45 40 42 40 32 43 36
34 53 38 40 39 32 45 40 50 45 40 40 26 45 40 45 35 40 42 45
(1)补全频率分布表和频率分布直方图.
分组 | 频数 | 频率 |
4.5﹣22.5 | 2 | 0.050 |
22.5﹣30.5 | 3 | |
30.5﹣38.5 | 10 | 0.250 |
38.5﹣46.5 | 19 | |
46.5﹣54.5 | 5 | 0.125 |
54.5﹣62.5 | 1 | 0.025 |
合计 | 40 | 1.000 |
(2)填空:在这个问题中,总体是____,样本是____.由统计结果分析的,这组数据的平均数是38.35(分),众数是____,中位数是_____.
(3)如果描述该校400名学生一周内平均每天参加课外锻炼时间的总体情况,你认为用平均数、众数、中位数中的哪一个量比较合适?
(4)估计这所学校有多少名学生,平均每天参加课外锻炼的时间多于30分?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小云想用7天的时间背诵若干首诗词,背诵计划如下:
①将诗词分成4组,第i组有![]() 首,i =1,2,3,4;
首,i =1,2,3,4;
②对于第i组诗词,第i天背诵第一遍,第(![]() )天背诵第二遍,第(
)天背诵第二遍,第(![]() )天背诵第三遍,三遍后完成背诵,其它天无需背诵,
)天背诵第三遍,三遍后完成背诵,其它天无需背诵,![]() 1,2,3,4;
1,2,3,4;
第1天 | 第2天 | 第3天 | 第4天 | 第5天 | 第6天 | 第7天 | |
第1组 |
|
|
| ||||
第2组 |
|
|
| ||||
第3组 | |||||||
第4组 |
|
|
|
③每天最多背诵14首,最少背诵4首.
解答下列问题:
(1)填入![]() 补全上表;
补全上表;
(2)若![]() ,
,![]() ,
,![]() ,则
,则![]() 的所有可能取值为______;
的所有可能取值为______;
(3)7天后,小云背诵的诗词最多为______首.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com