
【题目】在Rt△ABC中,∠ABC=90°,∠BAC=30°,将△ABC绕点A顺时针旋转一定的角度![]() 得到△AED,点B、C的对应点分别是E、D.
得到△AED,点B、C的对应点分别是E、D.
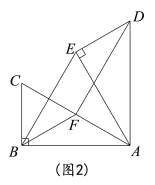
(1)如图1,当点E恰好在AC上时,求∠CDE的度数;
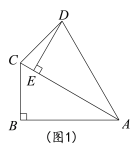
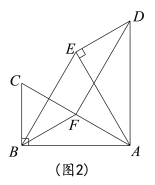
(2)如图2,若![]() =60°时,点F是边AC中点,求证:四边形BFDE是平行四边形.
=60°时,点F是边AC中点,求证:四边形BFDE是平行四边形.

【答案】(1)15°;(2)证明见解析.
【解析】
(1)如图1,利用旋转的性质得CA=DA,∠CAD=∠BAC=30°,∠DEA=∠ABC=90°,再根据等腰三角形的性质求出∠ADC,从而计算出∠CDE的度数;
(2)如图2,利用直角三角形斜边上的中线性质得到BF=![]() AC,利用含30度的直角三角形三边的关系得到BC=
AC,利用含30度的直角三角形三边的关系得到BC=![]() AC,则BF=BC,再根据旋转的性质得到∠BAE=∠CAD=60°,AB=AE,AC=AD ,DE=BC,从而得到DE=BF,△ACD和△BAE为等边三角形,接着由△AFD≌△CBA得到DF=BA,然后根据平行四边形的判定方法得到结论.
AC,则BF=BC,再根据旋转的性质得到∠BAE=∠CAD=60°,AB=AE,AC=AD ,DE=BC,从而得到DE=BF,△ACD和△BAE为等边三角形,接着由△AFD≌△CBA得到DF=BA,然后根据平行四边形的判定方法得到结论.
解:(1)如图1,∵△ABC绕点A顺时针旋转α得到△AED,点E恰好在AC上,
∴CA=CD,∠CAD=∠BAC=30°,∠DEA=∠ABC=90°,
∵CA=DA,
∴∠ACD=∠ADC=![]() (180°30°)=75°,∠ADE=90°-30°=60°,
(180°30°)=75°,∠ADE=90°-30°=60°,
∴∠CDE=75°60°=15°;
(2)证明:如图2,
∵点F是边AC中点,
∴BF=![]() AC,
AC,
∵∠BAC=30°,
∴BC=![]() AC,
AC,
∴BF=BC,
∵△ABC绕点A顺时针旋转60°得到△AED,
∴∠BAE=∠CAD=60°,AB=AE,AC=AD,DE=BC,
∴DE=BF,△ACD和△BAE为等边三角形,
∴BE=AB,
∵点F为△ACD的边AC的中点,
∴DF⊥AC,
易证得△AFD≌△CBA,
∴DF=BA,
∴DF=BE,
而BF=DE,
∴四边形BEDF是平行四边形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ,
,![]() 为常数)的图象经过点
为常数)的图象经过点![]() .
.
(1)求![]() ,
,![]() 满足的关系式;
满足的关系式;
(2)设该函数图象的顶点坐标是![]() ,当
,当![]() 的值变化时,求
的值变化时,求![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(3)若该函数的图象不经过第三象限,当![]() 时,函数的最大值与最小值之差为16,求
时,函数的最大值与最小值之差为16,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】黄石市在创建国家级文明卫生城市中,绿化档次不断提升.某校计划购进A,B两种树木共100棵进行校园绿化升级,经市场调查:购买A种树木2棵,B种树木5棵,共需600元;购买A种树木3棵,B种树木1棵,共需380元.
(1)求A种,B种树木每棵各多少元?
(2)因布局需要,购买A种树木的数量不少于B种树木数量的3倍.学校与中标公司签订的合同中规定:在市场价格不变的情况下(不考虑其他因素),实际付款总金额按市场价九折优惠,请设计一种购买树木的方案,使实际所花费用最省,并求出最省的费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,反比例函数![]() 的图象与一次函数
的图象与一次函数![]() 的图象交于点
的图象交于点![]() 、点
、点![]() .
.
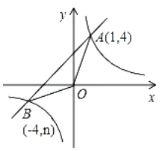
(1)求一次函数和反比例函数的解析式;
(2)求![]() 的面积;
的面积;
(3)直接写出一次函数值大于反比例函数值的自变量![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,二次函数的图像交坐标轴于A(-1,0),B(4,0),C(0,-4)三点,点P是直线BC下方抛物线上一动点.

(1)求这个二次函数的解析式;
(2)是否存在点P,使△POC是以OC为底边的等腰三角形?若存在,求出P点坐标;若不存在,请说明理由;
(3)动点P运动到什么位置时,△PBC面积最大,求出此时P点坐标和△PBC的最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
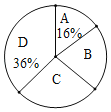
【题目】为宣传6月6日世界海洋日,某校九年级举行了主题为“珍惜海洋资源,保护海洋生物多样性”的知识竞赛活动.为了解全年级500名学生此次竞赛成绩(百分制)的情况,随机抽取了部分参赛学生的成绩,整理并绘制出如下不完整的统计表(表1)和统计图(如图).请根据图表信息解答以下问题:
(1)本次调查一共随机抽取了 个参赛学生的成绩;
(2)表1中![]() ;
;
(3)所抽取的参赛学生的成绩的中位数落在的“组别”是 ;
(4)请你估计,该校九年级竞赛成绩达到80分以上(含80分)的学生约有 人.
表1 知识竞赛成绩分组统计表
组别 | 分数/分 | 频数 |
A |
| a |
B |
| 10 |
C |
| 14 |
D |
| 18 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,我们将相同的两块含30°角的直角三角板Rt△DEF与Rt△ABC叠合,使DE在AB上,DE过点C,已知AC=DE=6.
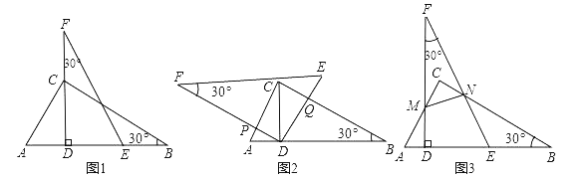
(1)将图1中的△DEF绕点D逆时针旋转(DF与AB不重合),使边DF、DE分别交AC、BC于点P、Q,如图2.
①求证:△CQD∽△APD;②连接PQ,设AP=x,求面积S△PCQ关于x的函数关系式;
(2)将图1中的△DEF向左平移(点A、D不重合),使边FD、FE分别交AC、BC于点M、N设AM=t,如图3.
①判断△BEN是什么三角形?并用含t的代数式表示边BE和BN;②连接MN,求面积S△MCN关于t的函数关系式;
(3)在旋转△DEF的过程中,试探求AC上是否存在点P,使得S△PCQ等于平移所得S△MCN的最大值?说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,![]() ,
,![]() 分别是
分别是![]() 两边的中点,如果
两边的中点,如果![]() 上的所有点都在△ABC的内部或边上,则称
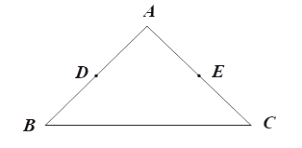
上的所有点都在△ABC的内部或边上,则称![]() 为△ABC的中内弧.例如,下图中
为△ABC的中内弧.例如,下图中![]() 是△ABC的一条中内弧.
是△ABC的一条中内弧.

(1)如图,在Rt△ABC中,![]() 分别是
分别是![]() 的中点.画出△ABC的最长的中内弧
的中点.画出△ABC的最长的中内弧![]() ,并直接写出此时
,并直接写出此时![]() 的长;
的长;
(2)在平面直角坐标系中,已知点![]() ,在△ABC中,
,在△ABC中,![]() 分别是
分别是![]() 的中点.
的中点.
①若![]() ,求△ABC的中内弧
,求△ABC的中内弧![]() 所在圆的圆心
所在圆的圆心![]() 的纵坐标的取值范围;
的纵坐标的取值范围;
②若在△ABC中存在一条中内弧![]() ,使得
,使得![]() 所在圆的圆心P在△ABC的内部或边上,直接写出t的取值范围.
所在圆的圆心P在△ABC的内部或边上,直接写出t的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com