
【题目】在△ABC中,![]() ,
,![]() 分别是
分别是![]() 两边的中点,如果
两边的中点,如果![]() 上的所有点都在△ABC的内部或边上,则称
上的所有点都在△ABC的内部或边上,则称![]() 为△ABC的中内弧.例如,下图中
为△ABC的中内弧.例如,下图中![]() 是△ABC的一条中内弧.
是△ABC的一条中内弧.

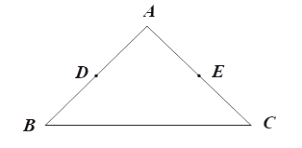
(1)如图,在Rt△ABC中,![]() 分别是
分别是![]() 的中点.画出△ABC的最长的中内弧
的中点.画出△ABC的最长的中内弧![]() ,并直接写出此时
,并直接写出此时![]() 的长;
的长;
(2)在平面直角坐标系中,已知点![]() ,在△ABC中,
,在△ABC中,![]() 分别是
分别是![]() 的中点.
的中点.
①若![]() ,求△ABC的中内弧
,求△ABC的中内弧![]() 所在圆的圆心
所在圆的圆心![]() 的纵坐标的取值范围;
的纵坐标的取值范围;
②若在△ABC中存在一条中内弧![]() ,使得
,使得![]() 所在圆的圆心P在△ABC的内部或边上,直接写出t的取值范围.
所在圆的圆心P在△ABC的内部或边上,直接写出t的取值范围.
【答案】(1)![]() ;(2)①P的纵坐标
;(2)①P的纵坐标![]() 或
或![]() ;②
;②![]() .
.
【解析】
(1)由三角函数值及等腰直角三角形性质可求得DE=2,最长中内弧即以DE为直径的半圆,![]() 的长即以DE为直径的圆周长的一半;
的长即以DE为直径的圆周长的一半;
(2)根据三角形中内弧定义可知,圆心一定在DE的中垂线上,,①当![]() 时,要注意圆心P在DE上方的中垂线上均符合要求,在DE下方时必须AC与半径PE的夹角∠AEP满足90°≤∠AEP<135°;②根据题意,t的最大值即圆心P在AC上时求得的t值.
时,要注意圆心P在DE上方的中垂线上均符合要求,在DE下方时必须AC与半径PE的夹角∠AEP满足90°≤∠AEP<135°;②根据题意,t的最大值即圆心P在AC上时求得的t值.
解:(1)如图2,
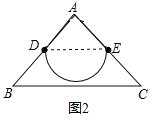
以DE为直径的半圆弧![]() ,就是△ABC的最长的中内弧
,就是△ABC的最长的中内弧![]() ,连接DE,∵∠A=90°,AB=AC=2
,连接DE,∵∠A=90°,AB=AC=2![]() ,D,E分别是AB,AC的中点,
,D,E分别是AB,AC的中点,![]() ,
,
∴弧![]()
![]() ;
;
(2)如图3,由垂径定理可知,圆心一定在线段DE的垂直平分线上,连接DE,作DE垂直平分线FP,作EG⊥AC交FP于G,

①当![]() 时,C(2,0),∴D(0,1),E(1,1),
时,C(2,0),∴D(0,1),E(1,1),![]() ,
,
设![]() 由三角形中内弧定义可知,圆心线段DE上方射线FP上均可,∴m≥1,
由三角形中内弧定义可知,圆心线段DE上方射线FP上均可,∴m≥1,
∵OA=OC,∠AOC=90°
∴∠ACO=45°,
∵DE∥OC
∴∠AED=∠ACO=45°
作EG⊥AC交直线FP于G,FG=EF=![]()
根据三角形中内弧的定义可知,圆心在点G的下方(含点G)直线FP上时也符合要求;
![]()
综上所述,![]() 或m≥1.
或m≥1.
②图4,设圆心P在AC上,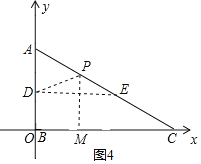
∵P在DE中垂线上,
∴P为AE中点,作PM⊥OC于M,则PM=![]()
![]() ,
,
∵DE∥BC
∴∠ADE=∠AOB=90°,
![]()
∵PD=PE,
∴∠AED=∠PDE
∵∠AED+∠DAE=∠PDE+∠ADP=90°,
∴∠DAE=∠ADP
![]()
由三角形中内弧定义知,PD≤PM
![]() ,AE≤3,即
,AE≤3,即![]() ,解得:
,解得:![]()



 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ABC=90°,∠BAC=30°,将△ABC绕点A顺时针旋转一定的角度![]() 得到△AED,点B、C的对应点分别是E、D.
得到△AED,点B、C的对应点分别是E、D.
(1)如图1,当点E恰好在AC上时,求∠CDE的度数;
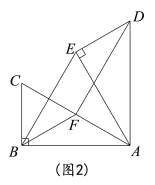
(2)如图2,若![]() =60°时,点F是边AC中点,求证:四边形BFDE是平行四边形.
=60°时,点F是边AC中点,求证:四边形BFDE是平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过x轴正半轴上的任意一点P,作y轴的平行线,分别与反比例函数![]() 和
和![]() 的图象交于A、B两点.若点C是y轴上任意一点,连接AC、BC,则△ABC的面积为( )
的图象交于A、B两点.若点C是y轴上任意一点,连接AC、BC,则△ABC的面积为( )
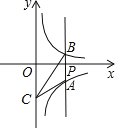
A. 3B. 4C. 5D. 10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△OAB如图所示放置在平面直角坐标系中,直角边OA与x轴重合,∠OAB=90°,OA=4,AB=2,把Rt△OAB绕点O逆时针旋转90°,点B旋转到点C的位置,抛物线y=ax2+bx经过点C、A.

(1)求该抛物线的解析式;
(2)在x轴上方的抛物线上有一动点P,过点P作x轴的平行线交抛物线于点M,分别过点P,点M作x轴的垂线,交x轴于R、S两点,问:四边形PRSM的周长是否有最大值?如果有,请求出最值,并写出解答过程;如果没有,请说明理由.
(3)在x轴上方的抛物线上是否存在点Q,过点Q作x轴的垂线,垂足为H,使得以O、Q、H为顶点的三角形与OAB相似,如果存在,直接写出点Q的坐标,如果不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小云想用7天的时间背诵若干首诗词,背诵计划如下:
①将诗词分成4组,第i组有![]() 首,i =1,2,3,4;
首,i =1,2,3,4;
②对于第i组诗词,第i天背诵第一遍,第(![]() )天背诵第二遍,第(
)天背诵第二遍,第(![]() )天背诵第三遍,三遍后完成背诵,其它天无需背诵,
)天背诵第三遍,三遍后完成背诵,其它天无需背诵,![]() 1,2,3,4;
1,2,3,4;
第1天 | 第2天 | 第3天 | 第4天 | 第5天 | 第6天 | 第7天 | |
第1组 |
|
|
| ||||
第2组 |
|
|
| ||||
第3组 | |||||||
第4组 |
|
|
|
③每天最多背诵14首,最少背诵4首.
解答下列问题:
(1)填入![]() 补全上表;
补全上表;
(2)若![]() ,
,![]() ,
,![]() ,则
,则![]() 的所有可能取值为______;
的所有可能取值为______;
(3)7天后,小云背诵的诗词最多为______首.
查看答案和解析>>
科目:初中数学 来源: 题型:
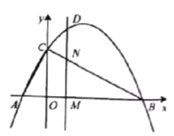
【题目】二次函数![]() 的图象交
的图象交![]() 轴于
轴于![]() 两点,交
两点,交![]() 轴于点
轴于点![]() .动点
.动点![]() 从点
从点![]() 出发,以每秒2个单位长度的速度沿
出发,以每秒2个单位长度的速度沿![]() 方向运动,过点
方向运动,过点![]() 作
作![]() 轴交直线
轴交直线![]() 于点
于点![]() ,交抛物线于点
,交抛物线于点![]() ,连接
,连接![]() .设运动的时间为
.设运动的时间为![]() 秒.
秒.
(1)求二次函数![]() 的表达式:
的表达式:
(2)连接![]() ,当
,当![]() 时,求
时,求![]() 的面积:
的面积:
(3)在直线![]() 上存在一点
上存在一点![]() ,当
,当![]() 是以
是以![]() 为直角的等腰直角三角形时,求此时点
为直角的等腰直角三角形时,求此时点![]() 的坐标;
的坐标;
(4)当![]() 时,在直线
时,在直线![]() 上存在一点
上存在一点![]() ,使得
,使得![]() ,求点
,求点![]() 的坐标
的坐标
查看答案和解析>>
科目:初中数学 来源: 题型:
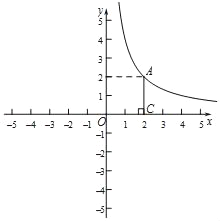
【题目】如图,在平面直角坐标系xOy中,函数y=![]() (x>0)的图象经过点A,作AC⊥x轴于点C.
(x>0)的图象经过点A,作AC⊥x轴于点C.
(1)求k的值;
(2)直线y=ax+b(a≠0)图象经过点A交x轴于点B,且OB=2AC.求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着城际铁路的开通,从甲市到乙市的高铁里程比快里程缩短了90千米,运行时间减少了8小时,已知甲市到乙市的普快列车里程为1220千米,高铁平均时速是普快平均时速的2.5倍.
(1)求高铁列车的平均时速;
(2)若从甲市到乙市途经丙市,且从甲市到丙市的高铁里程为780千米.某日王老师要从甲市去丙市参加14:00召开的会议,如果他买了当日10:00从甲市到丙市的高铁票,而且从丙市高铁站到会议地点最多需要0.5小时.试问在高铁列车准点到达的情况下,王老师能否在开会之前赶到会议地点?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com