
ЁОЬтФПЁПШчЭМЃЌRtЁїOABШчЭМЫљЪОЗХжУдкЦНУцжБНЧзјБъЯЕжаЃЌжБНЧБпOAгыxжсжиКЯЃЌЁЯOAB=90ЁуЃЌOA=4ЃЌAB=2ЃЌАбRtЁїOABШЦЕуOФцЪБеыа§зЊ90ЁуЃЌЕуBа§зЊЕНЕуCЕФЮЛжУЃЌХзЮяЯпy=ax2+bxОЙ§ЕуCЁЂA.

ЃЈ1ЃЉЧѓИУХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉдкxжсЩЯЗНЕФХзЮяЯпЩЯгавЛЖЏЕуPЃЌЙ§ЕуPзїxжсЕФЦНааЯпНЛХзЮяЯпгкЕуMЃЌЗжБ№Й§ЕуPЃЌЕуMзїxжсЕФДЙЯпЃЌНЛxжсгкRЁЂSСНЕуЃЌЮЪЃКЫФБпаЮPRSMЕФжмГЄЪЧЗёгазюДѓжЕЃПШчЙћгаЃЌЧыЧѓГізюжЕЃЌВЂаДГіНтД№Й§ГЬЃЛШчЙћУЛгаЃЌЧыЫЕУїРэгЩЃЎ
ЃЈ3ЃЉдкxжсЩЯЗНЕФХзЮяЯпЩЯЪЧЗёДцдкЕуQ,Й§ЕуQзїxжсЕФДЙЯпЃЌДЙзуЮЊH,ЪЙЕУвдOЁЂQЁЂHЮЊЖЅЕуЕФШ§НЧаЮгыOABЯрЫЦЃЌШчЙћДцдкЃЌжБНгаДГіЕуQЕФзјБъЃЌШчЙћВЛДцдкЃЌЧыЫЕУїРэгЩЁЃ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉгаЃЌзюДѓжЕЮЊ10ЃЌЙ§ГЬТдЃЛЃЈ3ЃЉДцдкЃЌQ1(2,4)ЃЛQ2 (
ЃЛЃЈ2ЃЉгаЃЌзюДѓжЕЮЊ10ЃЌЙ§ГЬТдЃЛЃЈ3ЃЉДцдкЃЌQ1(2,4)ЃЛQ2 (![]() ).
).
ЁОНтЮіЁП
ЃЈ1ЃЉИљОна§зЊЕФаджЪПЩЧѓГіCЕФзјБъКЭAЕФзјБъЃЌгжвђЮЊХзЮяЯпОЙ§дЕуЃЌЙЪЩшy=ax2+bxАбЃЈ2ЃЌ4ЃЉЃЌЃЈ4ЃЌ0ЃЉДњШыЃЌЧѓГіaКЭbЕФжЕМДПЩЧѓГіИУХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЫФБпаЮPRSMЕФжмГЄгазюДѓжЕЃЌЩшЕуPЕФзјБъЮЊPЃЈaЃЌ-a2+4aЃЉдђгЩХзЮяЯпЕФЖдГЦаджЊOR=ASЃЌЫљвдRS=PM=4-2aЃЌPR=MS=-a2+4aЃЌдђОиаЮPRSMЕФжмГЄL=2[4-2a+ЃЈ-a2+4aЃЉ]=-2ЃЈa-1ЃЉ2+10ЃЌРћгУКЏЪ§ЕФаджЪМДПЩЧѓГіЫФБпаЮPRSMЕФжмГЄЕФзюДѓжЕЃЎ
ЃЈ3ЃЉЗжБ№МЦЫуЁїOHQЁзЁїBAOКЭЁїOHQЁзЁїOABЪБQЕуЕФзјБъЃЌЗжЮіКѓМДПЩНтД№.
НтЃКЃЈ1ЃЉЁпOA=4ЃЌAB=2ЃЌЁїAOBШЦЕуOФцЪБеыа§зЊ90ЁуЃЌЕуBа§зЊЕНЕуCЕФЮЛжУЃЌЁрЕуCЕФзјБъЮЊЃЈ2ЃЌ4ЃЉЃЎ
гжЁпЕуAЕФзјБъЮЊЃЈ4ЃЌ0ЃЉЃЌХзЮяЯпОЙ§дЕуЃЌЙЪЩшy=ax2+bxЃЈaЁй0ЃЉЃЌАбЃЈ2ЃЌ4ЃЉЃЌЃЈ4ЃЌ0ЃЉДњШыЃЌЕУ![]() ЃЌ
ЃЌ
НтЕУ![]() ЃЌЫљвдХзЮяЯпЕФНтЮіЪНЮЊy=-x2+4xЃЛ
ЃЌЫљвдХзЮяЯпЕФНтЮіЪНЮЊy=-x2+4xЃЛ
ЃЈ2ЃЉгазюДѓжЕЃЎШчЭМЃЌ
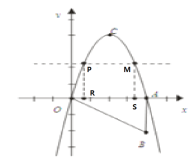
РэгЩШчЯТЃКЩшЕуPЕФзјБъЮЊPЃЈaЃЌ-a2+4aЃЉЃЌPR=MS=-a2+4aЃЌ
дђгЩХзЮяЯпЕФЖдГЦаджЊOR=ASЃЌЫљвдRS=PM=4-2aЃЌ
дђОиаЮPRSMЕФжмГЄL=2[4-2a+ЃЈ-a2+4aЃЉ]=-2ЃЈa-1ЃЉ2+10ЃЌ
ЫљвдЕБa=1ЪБЃЌОиаЮPRSMЕФжмГЄгазюДѓжЕЃЌLmax=10ЃЎ
ЃЈ3ЃЉЩшHЕузјБъЮЊЃЈnЃЌ0ЃЉ,дђOH=nЃЌQH=-n+4nЃЌ
ЂйМйЩшЁїOHQЁзЁїBAOЃЌдђ![]() ,
,
ПЩЕУ![]() ЃЌНтЕУ
ЃЌНтЕУ![]() =2ЃЌ
=2ЃЌ![]() =0ЃЈЩсШЅЃЉЃЌ
=0ЃЈЩсШЅЃЉЃЌ
ДњШыПЩЕУQЕузјБъЮЊЃЈ2ЃЌ4ЃЉЃЛ
ЂкМйЩшЁїOHQЁзЁїOABЃЌдђ![]() ,
,
![]() ЃЌНтЕУ
ЃЌНтЕУ![]() =
=![]() ЃЌ
ЃЌ![]() =0ЃЈЩсШЅЃЉЃЌ
=0ЃЈЩсШЅЃЉЃЌ
ДњШыПЩЕУQЕузјБъЮЊЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЛ
ЃЉЃЛ
злЩЯЫљЪіQЕузјБъЮЊЃЈ2ЃЌ4ЃЉЛђЃЈ![]() ЃЌ
ЃЌ![]() ЃЉ.
ЃЉ.


 ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ
ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКШчЭМЃЌЗДБШР§КЏЪ§![]() ЕФЭМЯѓгывЛДЮКЏЪ§
ЕФЭМЯѓгывЛДЮКЏЪ§![]() ЕФЭМЯѓНЛгкЕу
ЕФЭМЯѓНЛгкЕу![]() ЁЂЕу
ЁЂЕу![]() .
.
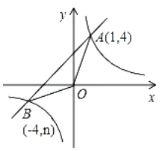
ЃЈ1ЃЉЧѓвЛДЮКЏЪ§КЭЗДБШР§КЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЧѓ![]() ЕФУцЛ§ЃЛ
ЕФУцЛ§ЃЛ
ЃЈ3ЃЉжБНгаДГівЛДЮКЏЪ§жЕДѓгкЗДБШР§КЏЪ§жЕЕФздБфСП![]() ЕФШЁжЕЗЖЮЇ.
ЕФШЁжЕЗЖЮЇ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌЮвУЧНЋЯрЭЌЕФСНПщКЌ30ЁуНЧЕФжБНЧШ§НЧАхRtЁїDEFгыRtЁїABCЕўКЯЃЌЪЙDEдкABЩЯЃЌDEЙ§ЕуCЃЌвбжЊACЃНDEЃН6ЃЎ
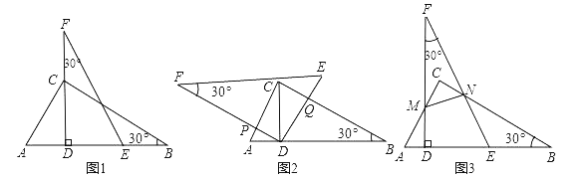
ЃЈ1ЃЉНЋЭМ1жаЕФЁїDEFШЦЕуDФцЪБеыа§зЊЃЈDFгыABВЛжиКЯЃЉЃЌЪЙБпDFЁЂDEЗжБ№НЛACЁЂBCгкЕуPЁЂQЃЌШчЭМ2ЃЎ
ЂйЧѓжЄЃКЁїCQDЁзЁїAPDЃЛЂкСЌНгPQЃЌЩшAPЃНxЃЌЧѓУцЛ§SЁїPCQЙигкxЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ2ЃЉНЋЭМ1жаЕФЁїDEFЯђзѓЦНвЦЃЈЕуAЁЂDВЛжиКЯЃЉЃЌЪЙБпFDЁЂFEЗжБ№НЛACЁЂBCгкЕуMЁЂNЩшAMЃНtЃЌШчЭМ3ЃЎ
ЂйХаЖЯЁїBENЪЧЪВУДШ§НЧаЮЃПВЂгУКЌtЕФДњЪ§ЪНБэЪОБпBEКЭBNЃЛЂкСЌНгMNЃЌЧѓУцЛ§SЁїMCNЙигкtЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ3ЃЉдка§зЊЁїDEFЕФЙ§ГЬжаЃЌЪдЬНЧѓACЩЯЪЧЗёДцдкЕуPЃЌЪЙЕУSЁїPCQЕШгкЦНвЦЫљЕУSЁїMCNЕФзюДѓжЕЃПЫЕУїФуЕФРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвЛДЮКЏЪ§![]() ЗжБ№НЛyжсЁЂxжсгкAЁЂBСНЕуЃЌХзЮяЯпy=Љx2+bx+cЙ§AЁЂBСНЕуЃЎ
ЗжБ№НЛyжсЁЂxжсгкAЁЂBСНЕуЃЌХзЮяЯпy=Љx2+bx+cЙ§AЁЂBСНЕуЃЎ
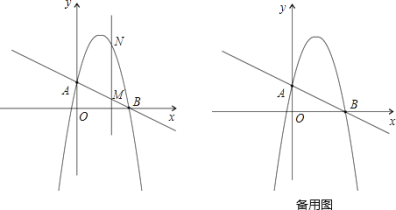
ЃЈ1ЃЉЧѓетИіХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉзїДЙжБxжсЕФжБЯпx=tЃЌдкЕквЛЯѓЯоНЛжБЯпABгкMЃЌНЛетИіХзЮяЯпгкNЃЎЧѓЕБtШЁКЮжЕЪБЃЌMNгазюДѓжЕЃПзюДѓжЕЪЧЖрЩйЃП
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЧщПіЯТЃЌвдAЁЂMЁЂNЁЂDЮЊЖЅЕузїЦНааЫФБпаЮЃЌЧѓЕкЫФИіЖЅЕуDЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЪаЮЊДДНЈШЋЙњЮФУїГЧЪаЃЌПЊеЙЁАУРЛЏТЬЛЏГЧЪаЁБЛюЖЏЃЌМЦЛЎОЙ§ШєИЩФъЪЙГЧЧјТЬЛЏзмУцЛ§аТді360ЭђЦНЗНУзЃЎзд2013ФъГѕПЊЪМЪЕЪЉКѓЃЌЪЕМЪУПФъТЬЛЏУцЛ§ЪЧдМЦЛЎЕФ1.6БЖЃЌетбљПЩЬсЧА4ФъЭъГЩШЮЮёЃЎ
ЃЈ1ЃЉЮЪЪЕМЪУПФъТЬЛЏУцЛ§ЖрЩйЭђЦНЗНУзЃП
ЃЈ2ЃЉЮЊМгДѓДДГЧСІЖШЃЌЪаеўИЎОіЖЈДг2016ФъЦ№МгПьТЬЛЏЫйЖШЃЌвЊЧѓВЛГЌЙ§2ФъЭъГЩЃЌФЧУДЪЕМЪЦНОљУПФъТЬЛЏУцЛ§жСЩйЛЙвЊдіМгЖрЩйЭђЦНЗНУзЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЙњМвДДаТжИЪ§ЪЧЗДгГвЛИіЙњМвПЦбЇММЪѕКЭДДаТОКељСІЕФзлКЯжИЪ§ЃЎЖдЙњМвДДаТжИЪ§ЕУЗжХХУћЧА40ЕФЙњМвЕФгаЙиЪ§ОнНјааЪеМЏЁЂећРэЁЂУшЪіКЭЗжЮіЃЎЯТУцИјГіСЫВПЗжаХЯЂЃК
aЃЎЙњМвДДаТжИЪ§ЕУЗжЕФЦЕЪ§ЗжВМжБЗНЭМЃЈЪ§ОнЗжГЩ7зщЃК
30ЁмxЃМ40ЃЌ40ЁмxЃМ50ЃЌ50ЁмxЃМ60ЃЌ60ЁмxЃМ70ЃЌ70ЁмxЃМ80ЃЌ80ЁмxЃМ90ЃЌ90ЁмxЁм100ЃЉЃЛ
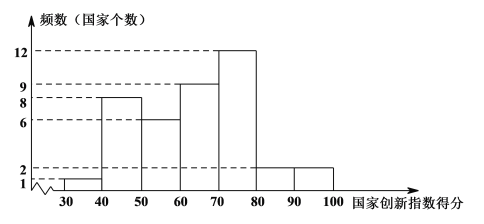
bЃЎЙњМвДДаТжИЪ§ЕУЗждк60ЁмxЃМ70етвЛзщЕФЪЧЃК61.7 62.4 63.6 65.9 66.4 68.5 69.1 69.3 69.5
cЃЎ40ИіЙњМвЕФШЫОљЙњФкЩњВњзмжЕКЭЙњМвДДаТжИЪ§ЕУЗжЧщПіЭГМЦЭМЃК
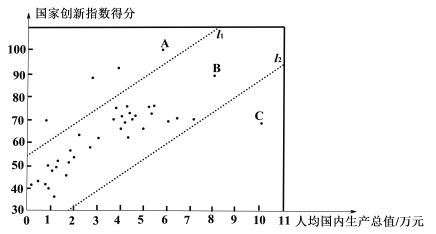
dЃЎжаЙњЕФЙњМвДДаТжИЪ§ЕУЗжЮЊ69.5.
ЃЈвдЩЯЪ§ОнРДдДгкЁЖЙњМвДДаТжИЪ§БЈИцЃЈ2018ЃЉЁЗЃЉ
ИљОнвдЩЯаХЯЂЃЌЛиД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉжаЙњЕФЙњМвДДаТжИЪ§ЕУЗжХХУћЪРНчЕк______ЃЛ
ЃЈ2ЃЉдк40ИіЙњМвЕФШЫОљЙњФкЩњВњзмжЕКЭЙњМвДДаТжИЪ§ЕУЗжЧщПіЭГМЦЭМжаЃЌАќРЈжаЙњдкФкЕФЩйЪ§МИИіЙњМвЫљЖдгІЕФЕуЮЛгкащЯп![]() ЕФЩЯЗНЃЎЧыдкЭМжагУЁА
ЕФЩЯЗНЃЎЧыдкЭМжагУЁА![]() ЁБШІГіДњБэжаЙњЕФЕуЃЛ
ЁБШІГіДњБэжаЙњЕФЕуЃЛ
ЃЈ3ЃЉдкЙњМвДДаТжИЪ§ЕУЗжБШжаЙњИпЕФЙњМвжаЃЌШЫОљЙњФкЩњВњзмжЕЕФзюаЁжЕдМЮЊ______ЭђУРдЊЃЛЃЈНсЙћБЃСєвЛЮЛаЁЪ§ЃЉ
ЃЈ4ЃЉЯТСаЭЦЖЯКЯРэЕФЪЧ______ЃЎ
ЂйЯрБШгкЕуAЃЌBЫљДњБэЕФЙњМвЃЌжаЙњЕФЙњМвДДаТжИЪ§ЕУЗжЛЙгавЛЖЈВюОрЃЌжаЙњЬсГіЁАМгПьНЈЩшДДаТаЭЙњМвЁБЕФеНТдШЮЮёЃЌНјвЛВНЬсИпЙњМвзлКЯДДаТФмСІЃЛ
ЂкЯрБШгкЕуBЃЌCЫљДњБэЕФЙњМвЃЌжаЙњЕФШЫОљЙњФкЩњВњзмжЕЛЙгавЛЖЈВюОрЃЌжаЙњЬсГіЁАОіЪЄШЋУцНЈГЩаЁПЕЩчЛсЁБЕФЗмЖЗФПБъЃЌНјвЛВНЬсИпШЫОљЙњФкЩњВњзмжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЁїABCжаЃЌ![]() ЃЌ
ЃЌ![]() ЗжБ№ЪЧ
ЗжБ№ЪЧ![]() СНБпЕФжаЕуЃЌШчЙћ
СНБпЕФжаЕуЃЌШчЙћ![]() ЩЯЕФЫљгаЕуЖМдкЁїABCЕФФкВПЛђБпЩЯЃЌдђГЦ
ЩЯЕФЫљгаЕуЖМдкЁїABCЕФФкВПЛђБпЩЯЃЌдђГЦ![]() ЮЊЁїABCЕФжаФкЛЁЃЎР§ШчЃЌЯТЭМжа
ЮЊЁїABCЕФжаФкЛЁЃЎР§ШчЃЌЯТЭМжа![]() ЪЧЁїABCЕФвЛЬѕжаФкЛЁЃЎ
ЪЧЁїABCЕФвЛЬѕжаФкЛЁЃЎ

ЃЈ1ЃЉШчЭМЃЌдкRtЁїABCжаЃЌ![]() ЗжБ№ЪЧ
ЗжБ№ЪЧ![]() ЕФжаЕуЃЎЛГіЁїABCЕФзюГЄЕФжаФкЛЁ
ЕФжаЕуЃЎЛГіЁїABCЕФзюГЄЕФжаФкЛЁ![]() ЃЌВЂжБНгаДГіДЫЪБ
ЃЌВЂжБНгаДГіДЫЪБ![]() ЕФГЄЃЛ
ЕФГЄЃЛ
ЃЈ2ЃЉдкЦНУцжБНЧзјБъЯЕжаЃЌвбжЊЕу![]() ЃЌдкЁїABCжаЃЌ
ЃЌдкЁїABCжаЃЌ![]() ЗжБ№ЪЧ
ЗжБ№ЪЧ![]() ЕФжаЕуЃЎ
ЕФжаЕуЃЎ
ЂйШє![]() ЃЌЧѓЁїABCЕФжаФкЛЁ
ЃЌЧѓЁїABCЕФжаФкЛЁ![]() ЫљдкдВЕФдВаФ
ЫљдкдВЕФдВаФ![]() ЕФзнзјБъЕФШЁжЕЗЖЮЇЃЛ
ЕФзнзјБъЕФШЁжЕЗЖЮЇЃЛ
ЂкШєдкЁїABCжаДцдквЛЬѕжаФкЛЁ![]() ЃЌЪЙЕУ
ЃЌЪЙЕУ![]() ЫљдкдВЕФдВаФPдкЁїABCЕФФкВПЛђБпЩЯЃЌжБНгаДГіtЕФШЁжЕЗЖЮЇЃЎ
ЫљдкдВЕФдВаФPдкЁїABCЕФФкВПЛђБпЩЯЃЌжБНгаДГіtЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈЩњЛюЙлВьЃЉМзЁЂввСНШЫТђВЫЃЌМзЯАЙпТђвЛЖЈжЪСПЕФВЫЃЌввЯАЙпТђвЛЖЈН№ЖюЕФВЫЃЌСНШЫУПДЮТђВЫЕФЕЅМлЯрЭЌЃЌР§ШчЃК
ВЫМл | ||
жЪСП | Н№Жю | |
Мз |
|
|
вв |
|
|
ВЫМл | ||
жЪСП | Н№Жю | |
Мз |
| ____дЊ |
вв | ____ЧЇПЫ |
|
ЃЈ1ЃЉЭъГЩЩЯБэЃЛ
ЃЈ2ЃЉМЦЫуМзСНДЮТђВЫЕФОљМлКЭввСНДЮТђВЫЕФОљМлЃЎЃЈОљМл![]() змН№ЖюзмжЪСПЃЉ
змН№ЖюзмжЪСПЃЉ
ЃЈЪ§бЇЫМПМЃЉЩшМзУПДЮТђжЪСПЮЊ![]() ЧЇПЫЕФВЫЃЌввУПДЮТђН№ЖюЮЊ
ЧЇПЫЕФВЫЃЌввУПДЮТђН№ЖюЮЊ![]() дЊЕФВЫЃЌСНДЮЕФЕЅМлЗжБ№ЪЧ
дЊЕФВЫЃЌСНДЮЕФЕЅМлЗжБ№ЪЧ![]() дЊ
дЊ![]() ЧЇПЫЁЂ
ЧЇПЫЁЂ![]() дЊ
дЊ![]() ЧЇПЫЃЌгУКЌга
ЧЇПЫЃЌгУКЌга![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЕФЪНзгЃЌЗжБ№БэЪОГіМзЁЂввСНДЮТђВЫЕФОљМл
ЕФЪНзгЃЌЗжБ№БэЪОГіМзЁЂввСНДЮТђВЫЕФОљМл![]() ЁЂ
ЁЂ![]() ЃЎБШНЯ
ЃЎБШНЯ![]() ЁЂ
ЁЂ![]() ЕФДѓаЁЃЌВЂЫЕУїРэгЩЃЎ
ЕФДѓаЁЃЌВЂЫЕУїРэгЩЃЎ
ЃЈжЊЪЖЧЈвЦЃЉФГДЌдкЯрОрЮЊ![]() ЕФМзЁЂввСНТыЭЗМфЭљЗЕКНаавЛДЮЃЌдкУЛгаЫЎСїЪБЃЌДЌЕФЫйЖШЮЊ
ЕФМзЁЂввСНТыЭЗМфЭљЗЕКНаавЛДЮЃЌдкУЛгаЫЎСїЪБЃЌДЌЕФЫйЖШЮЊ![]() ЫљашЪБМфЮЊЃКШчЙћЫЎСїЫйЖШЮЊ
ЫљашЪБМфЮЊЃКШчЙћЫЎСїЫйЖШЮЊ![]() ЪБЃЈ
ЪБЃЈ![]() ЃЉЃЌДЌЫГЫЎКНааЫйЖШЮЊЃЈ
ЃЉЃЌДЌЫГЫЎКНааЫйЖШЮЊЃЈ![]() ЃЉЃЌФцЫЎКНааЫйЖШЮЊЃЈ
ЃЉЃЌФцЫЎКНааЫйЖШЮЊЃЈ![]() ЃЉЃЌЫљашЪБМфЮЊ
ЃЉЃЌЫљашЪБМфЮЊ![]() ЧыНшМјЩЯУцЕФбаОПОбщЃЌБШНЯ
ЧыНшМјЩЯУцЕФбаОПОбщЃЌБШНЯ![]() ЁЂ
ЁЂ![]() ЕФДѓаЁЃЌВЂЫЕУїРэгЩЃЎ
ЕФДѓаЁЃЌВЂЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
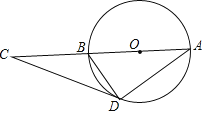
ЁОЬтФПЁПШчЭМЃЌCDЪЧЁбOЕФЧаЯпЃЌЕуCдкжБОЖABЕФбгГЄЯпЩЯЃЎ
ЃЈ1ЃЉЧѓжЄЃКЁЯCAD=ЁЯBDCЃЛ
ЃЈ2ЃЉШєBD=![]() ADЃЌAC=3ЃЌЧѓCDЕФГЄЃЎ
ADЃЌAC=3ЃЌЧѓCDЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com