
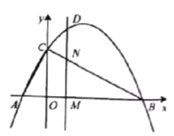
【题目】二次函数![]() 的图象交
的图象交![]() 轴于
轴于![]() 两点,交
两点,交![]() 轴于点
轴于点![]() .动点
.动点![]() 从点
从点![]() 出发,以每秒2个单位长度的速度沿
出发,以每秒2个单位长度的速度沿![]() 方向运动,过点
方向运动,过点![]() 作
作![]() 轴交直线
轴交直线![]() 于点
于点![]() ,交抛物线于点
,交抛物线于点![]() ,连接
,连接![]() .设运动的时间为
.设运动的时间为![]() 秒.
秒.
(1)求二次函数![]() 的表达式:
的表达式:
(2)连接![]() ,当
,当![]() 时,求
时,求![]() 的面积:
的面积:
(3)在直线![]() 上存在一点
上存在一点![]() ,当
,当![]() 是以
是以![]() 为直角的等腰直角三角形时,求此时点
为直角的等腰直角三角形时,求此时点![]() 的坐标;
的坐标;
(4)当![]() 时,在直线
时,在直线![]() 上存在一点
上存在一点![]() ,使得
,使得![]() ,求点
,求点![]() 的坐标
的坐标
【答案】(1)![]() (2)2(3)
(2)2(3)![]() (4)
(4)![]() 或
或![]()
【解析】
(1)直接将A、B两点的坐标代入列方程组解出即可;
(2)根据题意得出AM,OM,设![]() 的解析式为:
的解析式为:![]() ,将点
,将点![]() 代入求出解析式,然后将
代入求出解析式,然后将![]() 分别代入
分别代入![]() 和
和![]() 中,得:
中,得:![]() ,再根据三角形面积公式,即可解答
,再根据三角形面积公式,即可解答
(3)过点![]() 作
作![]() 轴的平行线,交
轴的平行线,交![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() 轴的平行线,交
轴的平行线,交![]() 的延长线于点
的延长线于点![]() ,设
,设![]() ,根据题意得出
,根据题意得出![]() ,根据
,根据![]() ,即可解答
,即可解答
(4)当![]() 时,
时,![]() ,此时
,此时![]() 点在二次函数的对称轴上,以
点在二次函数的对称轴上,以![]() 点为圆心,
点为圆心,![]() 长为半径作圆,交
长为半径作圆,交![]() 于
于![]() 两点,得出
两点,得出![]() ,再根据
,再根据![]() (同弧所对圆周角),即可解答
(同弧所对圆周角),即可解答
(1)将点![]() 代入
代入![]() ,得:
,得:
![]()
解得:
所以,二次函数的表达方式为:![]()
(2)![]()
又![]()
设![]() 的解析式为:
的解析式为:![]() ,将点
,将点![]() 代入,得:
代入,得:

所以,直线![]() 的解析式为:
的解析式为:![]() .
.
将![]() 分别代入
分别代入![]() 和
和![]() 中,得:
中,得:![]() .
.
![]()
![]() .
.
(3)假设过点![]() 作
作![]() 轴的平行线,交
轴的平行线,交![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() 轴的平行线,交
轴的平行线,交![]() 的延长线于点
的延长线于点![]() ,
,
设![]() ,由题意得:
,由题意得:
![]()
![]()

所以,点![]() 的坐标为:
的坐标为:![]()
(4)当![]() 时,
时,![]() ,此时
,此时![]() 点在二次函数的对称轴上,
点在二次函数的对称轴上,
以![]() 点为圆心,
点为圆心,![]() 长为半径作圆,交
长为半径作圆,交![]() 于
于![]() 两点
两点
![]()
![]()
![]() 点在该圆上
点在该圆上
![]()
![]()
![]() (同弧所对圆周角)
(同弧所对圆周角)
![]()
![]()
![]() 或
或![]()


科目:初中数学 来源: 题型:
【题目】某市为创建全国文明城市,开展“美化绿化城市”活动,计划经过若干年使城区绿化总面积新增360万平方米.自2013年初开始实施后,实际每年绿化面积是原计划的1.6倍,这样可提前4年完成任务.
(1)问实际每年绿化面积多少万平方米?
(2)为加大创城力度,市政府决定从2016年起加快绿化速度,要求不超过2年完成,那么实际平均每年绿化面积至少还要增加多少万平方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
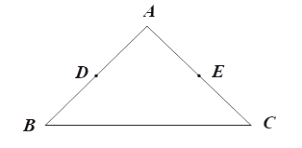
【题目】在△ABC中,![]() ,
,![]() 分别是
分别是![]() 两边的中点,如果
两边的中点,如果![]() 上的所有点都在△ABC的内部或边上,则称
上的所有点都在△ABC的内部或边上,则称![]() 为△ABC的中内弧.例如,下图中
为△ABC的中内弧.例如,下图中![]() 是△ABC的一条中内弧.
是△ABC的一条中内弧.

(1)如图,在Rt△ABC中,![]() 分别是
分别是![]() 的中点.画出△ABC的最长的中内弧
的中点.画出△ABC的最长的中内弧![]() ,并直接写出此时
,并直接写出此时![]() 的长;
的长;
(2)在平面直角坐标系中,已知点![]() ,在△ABC中,
,在△ABC中,![]() 分别是
分别是![]() 的中点.
的中点.
①若![]() ,求△ABC的中内弧
,求△ABC的中内弧![]() 所在圆的圆心
所在圆的圆心![]() 的纵坐标的取值范围;
的纵坐标的取值范围;
②若在△ABC中存在一条中内弧![]() ,使得
,使得![]() 所在圆的圆心P在△ABC的内部或边上,直接写出t的取值范围.
所在圆的圆心P在△ABC的内部或边上,直接写出t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
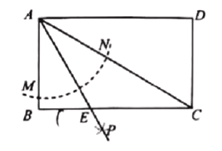
【题目】如图,矩形![]() 以点
以点![]() 为圆心,以任意长为半径作弧分别交
为圆心,以任意长为半径作弧分别交![]() 、
、![]() 于
于![]() 两点,再分别以点
两点,再分别以点![]() 为圆心,以大于
为圆心,以大于![]() 的长为半径作弧交于点
的长为半径作弧交于点![]() ,作射线
,作射线![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,则矩形
,则矩形![]() 的面积等于__________.
的面积等于__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(生活观察)甲、乙两人买菜,甲习惯买一定质量的菜,乙习惯买一定金额的菜,两人每次买菜的单价相同,例如:
菜价 | ||
质量 | 金额 | |
甲 |
|
|
乙 |
|
|
菜价 | ||
质量 | 金额 | |
甲 |
| ____元 |
乙 | ____千克 |
|
(1)完成上表;
(2)计算甲两次买菜的均价和乙两次买菜的均价.(均价![]() 总金额总质量)
总金额总质量)
(数学思考)设甲每次买质量为![]() 千克的菜,乙每次买金额为
千克的菜,乙每次买金额为![]() 元的菜,两次的单价分别是
元的菜,两次的单价分别是![]() 元
元![]() 千克、
千克、![]() 元
元![]() 千克,用含有
千克,用含有![]() 、
、![]() 、
、![]() 、
、![]() 的式子,分别表示出甲、乙两次买菜的均价
的式子,分别表示出甲、乙两次买菜的均价![]() 、
、![]() .比较
.比较![]() 、
、![]() 的大小,并说明理由.
的大小,并说明理由.
(知识迁移)某船在相距为![]() 的甲、乙两码头间往返航行一次,在没有水流时,船的速度为
的甲、乙两码头间往返航行一次,在没有水流时,船的速度为![]() 所需时间为:如果水流速度为
所需时间为:如果水流速度为![]() 时(
时(![]() ),船顺水航行速度为(
),船顺水航行速度为(![]() ),逆水航行速度为(
),逆水航行速度为(![]() ),所需时间为
),所需时间为![]() 请借鉴上面的研究经验,比较
请借鉴上面的研究经验,比较![]() 、
、![]() 的大小,并说明理由.
的大小,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的抛物线对称轴是直线x=1,与x轴有两个交点,与y轴交点坐标是(0,3),把它向下平移2个单位后,得到新的抛物线解析式是 y=ax2+bx+c,以下四个结论:①b2﹣4ac<0,②abc<0,③4a+2b+c=1,④a﹣b+c>0中,判断正确的有( )
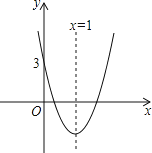
A. ②③④B. ①②③C. ②③D. ①④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人用如图的两个分格均匀的转盘![]() 做游戏,游戏规则如下:分别转动两个转盘,转盘停止后,指针分别指向一个数字(若指针停止在等份线上,那么重转一次,直到指针指向某一数字为止).用所指的两个数字相乘,如果积是奇数,则甲获胜;如果积是偶数,则乙获胜.请你解决下列问题:求甲、乙两人获胜的概率.
做游戏,游戏规则如下:分别转动两个转盘,转盘停止后,指针分别指向一个数字(若指针停止在等份线上,那么重转一次,直到指针指向某一数字为止).用所指的两个数字相乘,如果积是奇数,则甲获胜;如果积是偶数,则乙获胜.请你解决下列问题:求甲、乙两人获胜的概率.
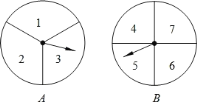
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形OABC的边OC、OA分别位于x、y轴上,点A(0,﹣4)、B(6,﹣4)、C(6,0),抛物线y=ax2+bx经过点O和点C,顶点M(3,﹣![]() ),点N是抛物线上一动点,直线MN交直线AB于点E,交y轴于F,△A′EF是将△AEF沿直线MN翻折后的图形.
),点N是抛物线上一动点,直线MN交直线AB于点E,交y轴于F,△A′EF是将△AEF沿直线MN翻折后的图形.
(1)求抛物线的解析式;
(2)当四边AEA′F是正方形时,求点N的坐标.
(3)连接CA′,求CA′的最小值.
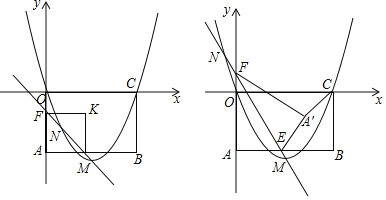
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com