
【题目】如图,过x轴正半轴上的任意一点P,作y轴的平行线,分别与反比例函数![]() 和
和![]() 的图象交于A、B两点.若点C是y轴上任意一点,连接AC、BC,则△ABC的面积为( )
的图象交于A、B两点.若点C是y轴上任意一点,连接AC、BC,则△ABC的面积为( )
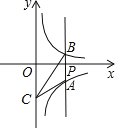
A. 3B. 4C. 5D. 10
科目:初中数学 来源: 题型:
【题目】黄石市在创建国家级文明卫生城市中,绿化档次不断提升.某校计划购进A,B两种树木共100棵进行校园绿化升级,经市场调查:购买A种树木2棵,B种树木5棵,共需600元;购买A种树木3棵,B种树木1棵,共需380元.
(1)求A种,B种树木每棵各多少元?
(2)因布局需要,购买A种树木的数量不少于B种树木数量的3倍.学校与中标公司签订的合同中规定:在市场价格不变的情况下(不考虑其他因素),实际付款总金额按市场价九折优惠,请设计一种购买树木的方案,使实际所花费用最省,并求出最省的费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,我们将相同的两块含30°角的直角三角板Rt△DEF与Rt△ABC叠合,使DE在AB上,DE过点C,已知AC=DE=6.
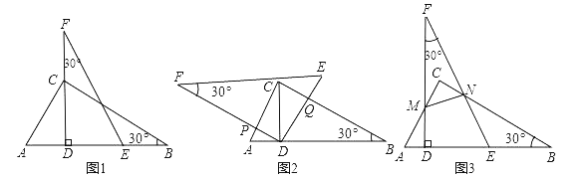
(1)将图1中的△DEF绕点D逆时针旋转(DF与AB不重合),使边DF、DE分别交AC、BC于点P、Q,如图2.
①求证:△CQD∽△APD;②连接PQ,设AP=x,求面积S△PCQ关于x的函数关系式;
(2)将图1中的△DEF向左平移(点A、D不重合),使边FD、FE分别交AC、BC于点M、N设AM=t,如图3.
①判断△BEN是什么三角形?并用含t的代数式表示边BE和BN;②连接MN,求面积S△MCN关于t的函数关系式;
(3)在旋转△DEF的过程中,试探求AC上是否存在点P,使得S△PCQ等于平移所得S△MCN的最大值?说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校计划为“我和我的祖国”演讲比赛购买奖品.已知购买3个A奖品和2个B奖品共需120元;购买5个A奖品和4个B奖品共需210元.
(1)求A,B两种奖品的单价;
(2)学校准备购买A,B两种奖品共30个,且A奖品的数量不少于B奖品数量的![]() .请设计出最省钱的购买方案,并说明理由.
.请设计出最省钱的购买方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 分别交y轴、x轴于A、B两点,抛物线y=﹣x2+bx+c过A、B两点.
分别交y轴、x轴于A、B两点,抛物线y=﹣x2+bx+c过A、B两点.
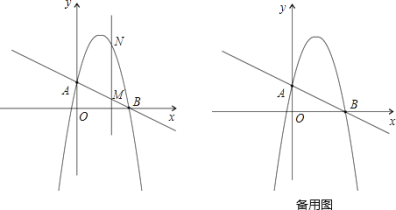
(1)求这个抛物线的解析式;
(2)作垂直x轴的直线x=t,在第一象限交直线AB于M,交这个抛物线于N.求当t取何值时,MN有最大值?最大值是多少?
(3)在(2)的情况下,以A、M、N、D为顶点作平行四边形,求第四个顶点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为创建全国文明城市,开展“美化绿化城市”活动,计划经过若干年使城区绿化总面积新增360万平方米.自2013年初开始实施后,实际每年绿化面积是原计划的1.6倍,这样可提前4年完成任务.
(1)问实际每年绿化面积多少万平方米?
(2)为加大创城力度,市政府决定从2016年起加快绿化速度,要求不超过2年完成,那么实际平均每年绿化面积至少还要增加多少万平方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,![]() ,
,![]() 分别是
分别是![]() 两边的中点,如果
两边的中点,如果![]() 上的所有点都在△ABC的内部或边上,则称
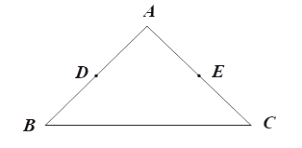
上的所有点都在△ABC的内部或边上,则称![]() 为△ABC的中内弧.例如,下图中
为△ABC的中内弧.例如,下图中![]() 是△ABC的一条中内弧.
是△ABC的一条中内弧.

(1)如图,在Rt△ABC中,![]() 分别是
分别是![]() 的中点.画出△ABC的最长的中内弧
的中点.画出△ABC的最长的中内弧![]() ,并直接写出此时
,并直接写出此时![]() 的长;
的长;
(2)在平面直角坐标系中,已知点![]() ,在△ABC中,
,在△ABC中,![]() 分别是
分别是![]() 的中点.
的中点.
①若![]() ,求△ABC的中内弧
,求△ABC的中内弧![]() 所在圆的圆心
所在圆的圆心![]() 的纵坐标的取值范围;
的纵坐标的取值范围;
②若在△ABC中存在一条中内弧![]() ,使得
,使得![]() 所在圆的圆心P在△ABC的内部或边上,直接写出t的取值范围.
所在圆的圆心P在△ABC的内部或边上,直接写出t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
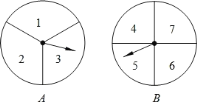
【题目】甲、乙两人用如图的两个分格均匀的转盘![]() 做游戏,游戏规则如下:分别转动两个转盘,转盘停止后,指针分别指向一个数字(若指针停止在等份线上,那么重转一次,直到指针指向某一数字为止).用所指的两个数字相乘,如果积是奇数,则甲获胜;如果积是偶数,则乙获胜.请你解决下列问题:求甲、乙两人获胜的概率.
做游戏,游戏规则如下:分别转动两个转盘,转盘停止后,指针分别指向一个数字(若指针停止在等份线上,那么重转一次,直到指针指向某一数字为止).用所指的两个数字相乘,如果积是奇数,则甲获胜;如果积是偶数,则乙获胜.请你解决下列问题:求甲、乙两人获胜的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com